3 ways number bonds lead to maths mastery

On a basic level, they provide a solid foundation for understanding how numbers can be split and combined. But over the long term, number bonds do a lot more — they give students an informed skill set for gaining mathematical fluency and navigating increasingly difficult concepts.

Here are three key reasons why number bonds are an essential tool for teaching maths mastery.

1. Number bonds give a tactile understanding of numbers

Students often struggle with mathematics because they struggle with abstraction. Enter the CPA method.

The CPA method is based on Jerome Bruner’s foundational enactive/iconic/symbolic concept (more commonly referred to as CPA — concrete/pictorial/abstract). A mainstay of maths teaching in Singapore, the CPA approach helps students master new ideas by introducing abstract concepts in a tactile, physical way. Through three steps, students master new concepts via physical objects, pictorial representations, and conventional abstract methods.

Here’s what it is, and how to use it with number bonds.

Concrete

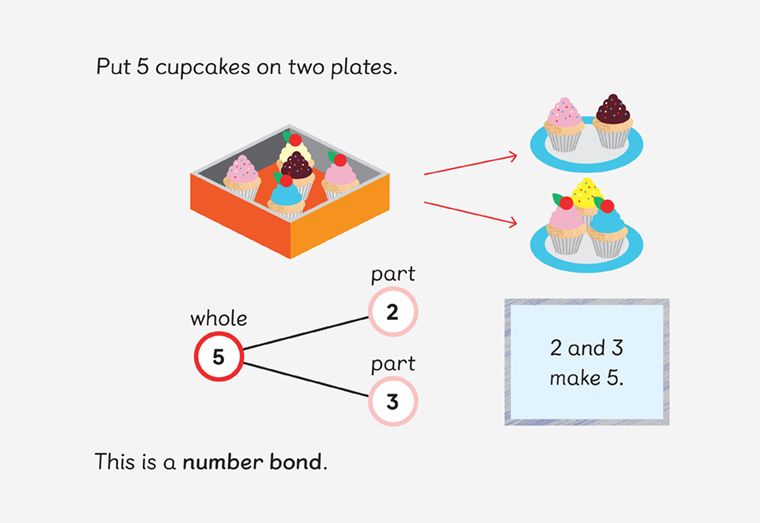
The concrete stage brings abstract concepts to life via physical objects. This is often referred to as the “doing” stage. Instead of being shown how to solve a problem, children are introduced to concepts by handling physical objects.

For example, provide a student with five apples. In how many different ways can they separate the apples onto two plates? Do the two plates combined still add up to five? This exercise shows students the different ways that numbers can be combined or split up.

Here’s another example.

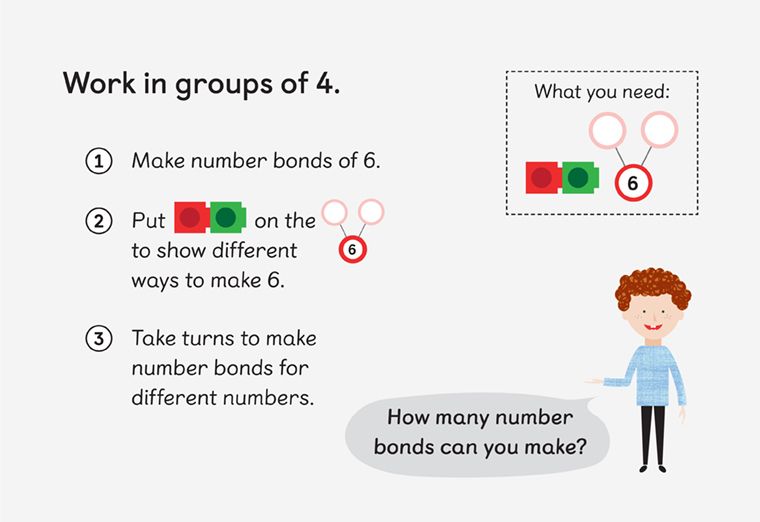
Pictorial

Pictorial exercises act as a bridge between tangible, concrete problems and abstract ones. This is the “seeing” stage of CPA approach.

The progress from concrete to pictorial is gradual. For example, you might first replace real apples with physical models (like cubes) to represent the apples. From there, use pictures to represent the cubes.

Familiar images, models, or diagrams encourage students to mentally connect familiar physical objects (like apples) with more abstract objects (like cubes and pictures of cubes). It’s just like the concrete stage, except the tangible objects are being represented with models, and not physically handled.

Abstract

With concrete and pictorial exercises mastered, students progress to the abstract step. This is the “symbolic” stage where teachers introduce symbolic numbers, notation, and mathematical symbols.

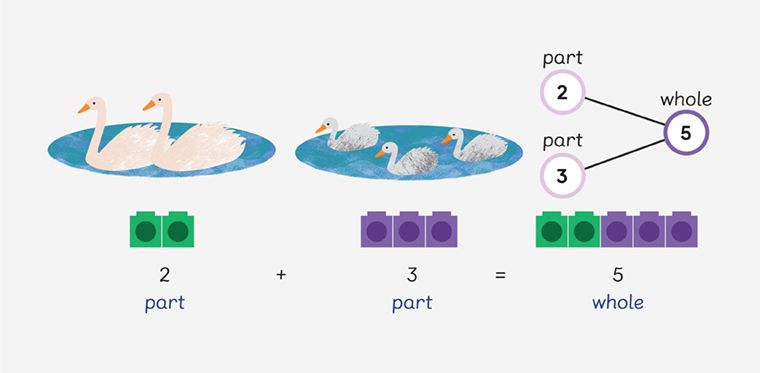
Having moved from concrete examples to pictorial ones, students make efficient connections between abstract examples and the concrete foundations they started with.

When it comes to mastering abstraction, variety is key. Each time a new maths idea is introduced, start with a concrete model and gradually move to pictorial representations before arriving at abstract symbols. Reinforcing the journey through the stages encourages a stronger mental connection between each phase.

Here’s another exercise. Afterwards, encourage pupils to write out the same story using numeric symbols and number bonds.

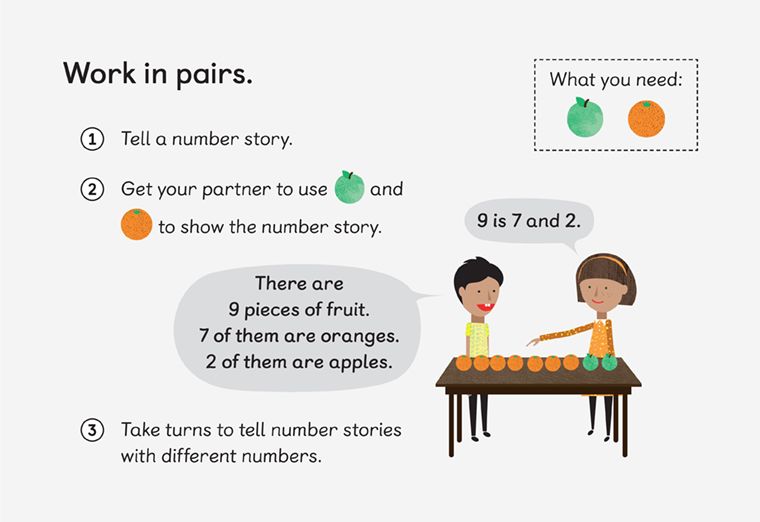
2. Number bonds develop mathematical fluency

Mathematical fluency is the capacity for conceptual understanding and the ability to accurately recall and apply knowledge. A stated objective of the National Curriculum, it’s a critical element of maths mastery.

With rote teaching methods, pupils memorize how to quickly recall addition or multiplication facts, but that’s not mathematical fluency. So how do you build mathematical fluency in your classroom?

Think about language. With language, the speed that we speak at doesn’t makes us fluent. It’s our ability to understand, reorganize, and combine different elements of language together to form coherent, complex sentences.

The same goes for math! Fluency allows students to understand how numbers and concepts work, and how to reorganize and apply them in changing contexts.

Number bonds are a crucial step to getting there. By learning how numbers can be split up and combined in useful ways, students gain a strong number sense; an intuitive understanding of numbers and the ability to make mental calculations.

A critical component of mathematical fluency, number sense allows students to tackle increasingly complicated problems and concepts without feeling lost.

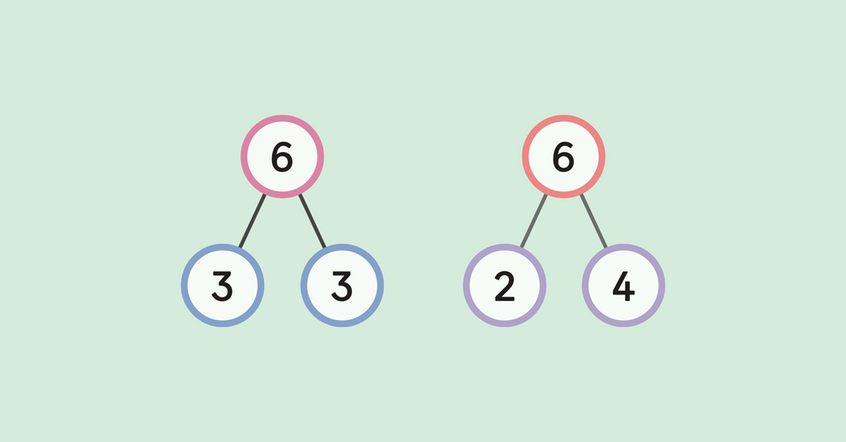
3. Number bonds make learning algorithms meaningful

Number bonds can develop what Richard Skemp calls “relational understanding” — the knowledge of how rules and procedures work. This is in opposition to procedural understanding — the memorization of rules and procedures (but not how they work).

Number bonds foster relational understanding, and help students understand how different algorithms work and why. That means less reliance on rote memorization, where students are more likely to make mistakes, forget techniques over time, or feel lost when faced with fresh concepts.

Effectively, number bonds give students the tools necessary to decode or unlock algorithms — a crucial component of understanding concepts on a deep level, and an important step towards math mastery.

Here’s an example of how number bonds can lead to relational understanding.

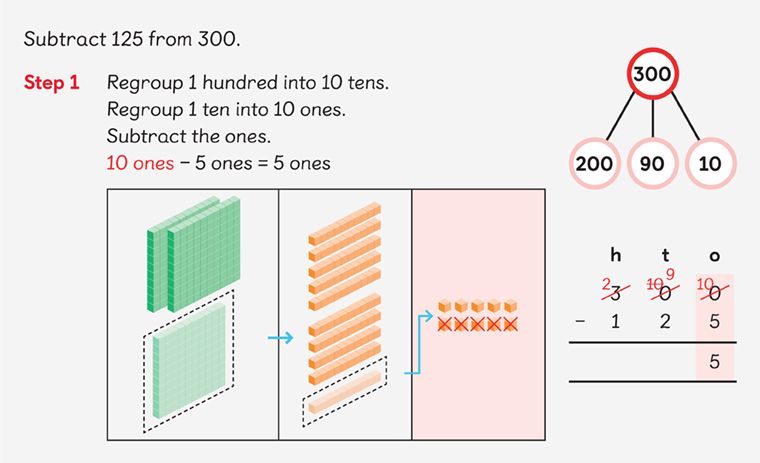
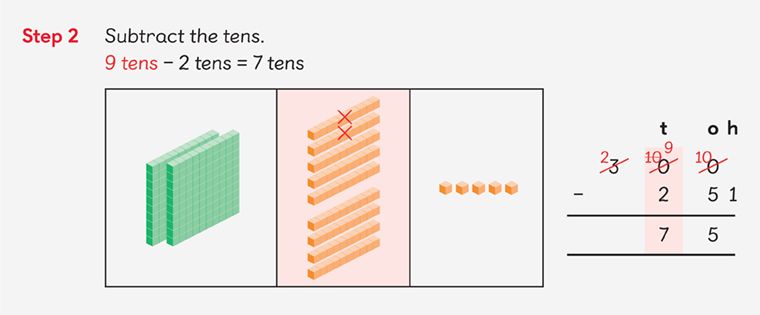
Further Resources

Looking to get the number bonds ball rolling in your classroom? Give these a try.

Learn more about the basics of number bonds.

Introduction to the CPA Approach

Early years maths mastery: introducing the CPA approach

Numbers Bonds With Dr. Yeap Ban Har