How to address common fractions misconceptions
Editor’s Note:
This is an updated version of a blog post published on 19 October, 2020
Understanding fractions is essential to understanding maths generally. But common misconceptions can leave both teachers and learners feeling more unsure than they should.
While it’s true you may not notice misconceptions in every primary maths lesson or with every child, knowing what common misconceptions look like and how to address them can make a significant difference in your learners’ understanding.
Let’s look at some common misconceptions in fractions and how the very early ideas about fractions are essential in forming firm foundations.
Common misconception 1: not understanding the denominator
A common misconception is that learners believe the numerator and denominator are the same. Let’s start with the fractions basics to help address this misconception.
‘Denominator’ means ‘that which names’ in Latin. This translation identifies the denominator as a name the same way ‘one’, ‘two’ and ‘three’ are names.
The denominator can also tell you the size of the parts. Children learn that:
*⁄2 shows us that each part is called a half and two of them will make one whole.
*⁄3 shows us that each part is called a third and three of them will make one whole.
*⁄4 shows us that each part is called a quarter and four of them will make one whole.
And so on.
Children need to use physical materials to discover this for themselves, like in the following example from Maths — No Problem! Textbook 1B, Chapter 14, Lesson 1.

How do we know that Charles’ part is the same as Holly’s part?
We could put Charles’ piece on Holly’s piece to see if they are the same size.
How many parts are needed to make one whole piece of paper?
It would take two parts to make one whole piece of paper.
Children need to discover this using physical materials first and develop the language associated with the idea.
For example take Maths — No Problem! Textbook 1B, Chapter 14, Lesson 2.

If we concentrate on the size of the pieces and understand that each size has a name, in this case a ‘quarter’, the notation becomes easier to understand.
Once learners understand this, we can find the name of the fraction.

What fraction of the shape is green?
Using the ideas that were first introduced in Year 1, this should be quite straightforward to answer.
It takes 6 green pieces to cover the yellow shape. There is one green piece.
1⁄6 of the shape is green. We can develop the idea further and ask, “How many green pieces would it take to cover half of the shape?”.
If we concentrate on the denominator first, the understanding of the numerator becomes easier to understand. The numerator is simply showing us the number of parts.
3⁄4 shows us that there are three parts and it takes four parts to make one whole.
Common misconception 2: why is 1⁄4 smaller than a 1⁄2?
Children learn that 4 is greater than 2. And this is true. So does it also hold true that 1⁄4 is greater than 1⁄2?
If you understand the role of the denominator, then this fraction misconception should not exist. However, when you do see this misconception, there are steps you can take:
1. Make the fraction using square or rectangular paper.
2. Cut out the pieces.
3. Compare the pieces to the written fractions.
Can a learner make the connection between the number of pieces it takes to make one whole, and the size of the pieces? Once that connection is made, and the learner has an understanding of what the denominator is telling us, the learner will see that one quarter is smaller than one half. We could go on to generalise and say ‘the smaller the part is, the more parts will be needed to make one whole’.
Common misconception 3: the language of fractions
We may learn procedures that are efficient and make working with fractions easier, but how well are they understood?
Let’s look at this Year 6 example in Maths — No Problem! Textbook 6A, Chapter 3, Lesson 15 which suggests that 3⁄4 ÷ 2 is equal to 1⁄2 × 3⁄4.
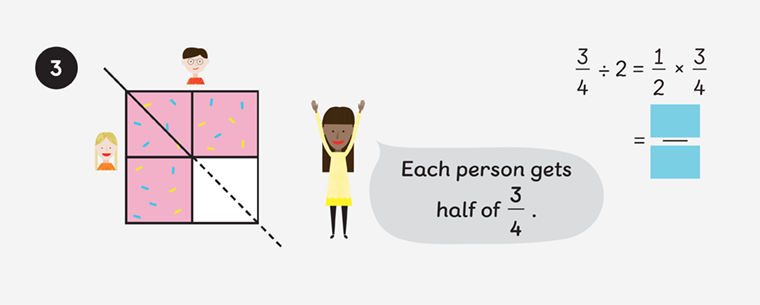
We’re able to teach the relationship between ÷ 2 and × 1⁄2 through the use of a procedure. But we want learners to understand why it works. In this case reading maths is helpful.
Why do ÷ 2 and × 1⁄2 have equivalence in the equation above?
Let’s complete part of the equation 3⁄4 ÷ 2 = 3⁄8, then read it as a sentence.
“Three quarters of a cake is shared between two people and each person receives 3⁄8 of the whole cake.”
And another part of the equation.
1⁄2 × 3⁄4 = 3⁄8
“Half of three quarters, or the remainder of the cake, is three eighths of the whole cake.
Each person receives three eighths of the cake.”
If children are struggling with this idea we can make a physical representation or show the representation pictorially as set out below.
3 × 4 = 3 groups of 4

2 × 4 = 2 groups of 4

1 × 4 = 1 group of 4

1⁄2 × 4 = 1⁄2 a group of 4

The final stage is giving the learner the opportunity to relate dividing 2 and multiplying by 1⁄2.
Common misconception 4: which numbers are added or subtracted?
If we understand the role of the denominator then we are unlikely to run into problems with adding and subtracting fractions. However, we need to be aware that learners may run into problems when faced with different denominators. We may see examples like:
6⁄8 − 1⁄4 = 5⁄4
The misconception here is not understanding that the denominator is a noun and we can only add or subtract the same noun.
In the same way we have to make an adjustment for the following problem:
There are 7 pieces of fruit in a bowl. Ravi takes 2 pieces. How many pieces of fruit are left in the bowl?

We need to see each of the items as a piece of fruit, not an apple or a banana, in order to complete the subtraction.
So with 7⁄8 − 1⁄4 = 5⁄4
We need the same denominator, fractions with the same name.
7⁄8 − 1⁄4 becomes 7⁄8 − 2⁄8
We read this as, “I have seven eighths and I take away two eights. I am left with five eighths.”
Understanding that many common fractions misconceptions originate from early ideas stresses the importance of getting these ideas well established and understood. This may take time but it builds a foundation that ensures the children can continue to learn and understand the many other new ideas in mathematics
Fractions for Mastery CPD
Would you like to gain confidence with fractions? This advanced, one-day course will give you the boost you need. Learn from one of our friendly experts in a relaxed, face-to-face setting.