Number Bonds

What is a number bond?

Number bonds let students split numbers in useful ways. They show how numbers join together, and how they break down into component parts. When used in Year 1, number bonds forge the number sense needed for early primary students to move to addition and subtraction. As students progress, number bonds become an essential mental problem-solving strategy.

Why are number bonds part of Singapore mathematics?

Number bonds are an essential component when teaching the Singapore method of maths for mastery. They foster number sense in students, and are an important concept within the Singapore primary curriculum. However so-called ‘Singapore Number Bonds’ are not a specifically Singaporean method — the term has been around since the 1920s.

How do number bonds work?

Number bonds are represented by circles connected by lines. The ‘whole’ is written in the first circle, while the ‘parts’ are in the adjoining circles.

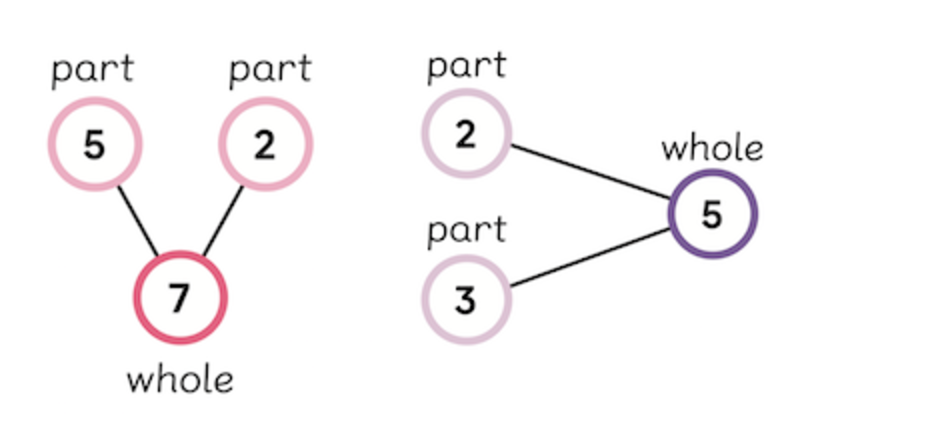
How to teach number bonds

Children are usually introduced to number bonds through the Concrete, Pictorial, Abstract (CPA) approach. Here’s just one way to introduce and teach number bonds.

Concrete step

Children start out by counting familiar real-world objects that they can interact with. They then use counters to represent the real-world objects. From here, they progress to grouping counters into two groups.

By putting five counters into two groups, children learn the different ways that five can be made. For example, 3 and 2 as illustrated below. With further exploration, children work out other ways to break numbers into two groups.

Pictorial step

Now that they understand the concept with hands-on objects and experience, children progress to writing number bonds in workbooks or on whiteboards. Early number bond explorations might simply reflect the two groups of counters that they created during the concrete step, along with other combinations.

Abstract step

With the concrete and pictorial steps done and dusted, children progress to representing abstract problems using mathematical notation (for example, 3 + 2 = 5).

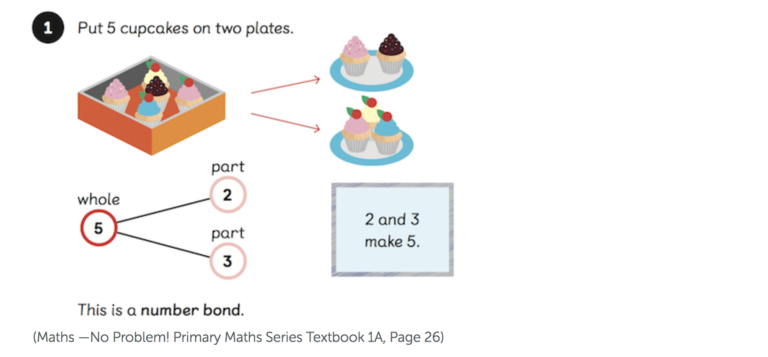
Taking the concept a step further

Number bonds also develop problem-solving strategies such as ‘making ten’ with ten frames, multilink or unifix cubes.

By mastering number bonds early on, pupils build the foundations needed for subsequent learning and are better equipped to develop mental strategies and mathematical fluency. By building a strong number sense, pupils can decide what action to take when trying to solve problems in their head.

This example shows how a pupil would develop their number sense, or mathematical fluency, by using number bonds to perform a mental calculation.