SOLO picks up where Bloom’s Taxonomy leaves off

“SOLO isn’t a hierarchy, but a series of stages. It suggests that learning is a cycle rather than a linear process of steps, and that learners can move to any part of the taxonomy, from the Quantity phase to the Quality phase, and back again.”

A couple of years ago, I conducted a Twitter poll that showed 80% of teaching staff knowingly use a taxonomy. The most common was Bloom’s Taxonomy, but a quarter of respondents used one called Structure of the Observed Learning Outcome (SOLO). Personally, I’m a big fan of SOLO.

So what is SOLO Taxonomy and why does it work so well in the maths mastery classroom?

What is the SOLO taxonomy?

SOLO was developed as a taxonomy in 1982 by John Biggs and Kevin Collis as an alternative to Bloom’s cognitive domain. Looking at the range of responses and outcomes that learners produce, they determined that the following structure is common to all subject areas.

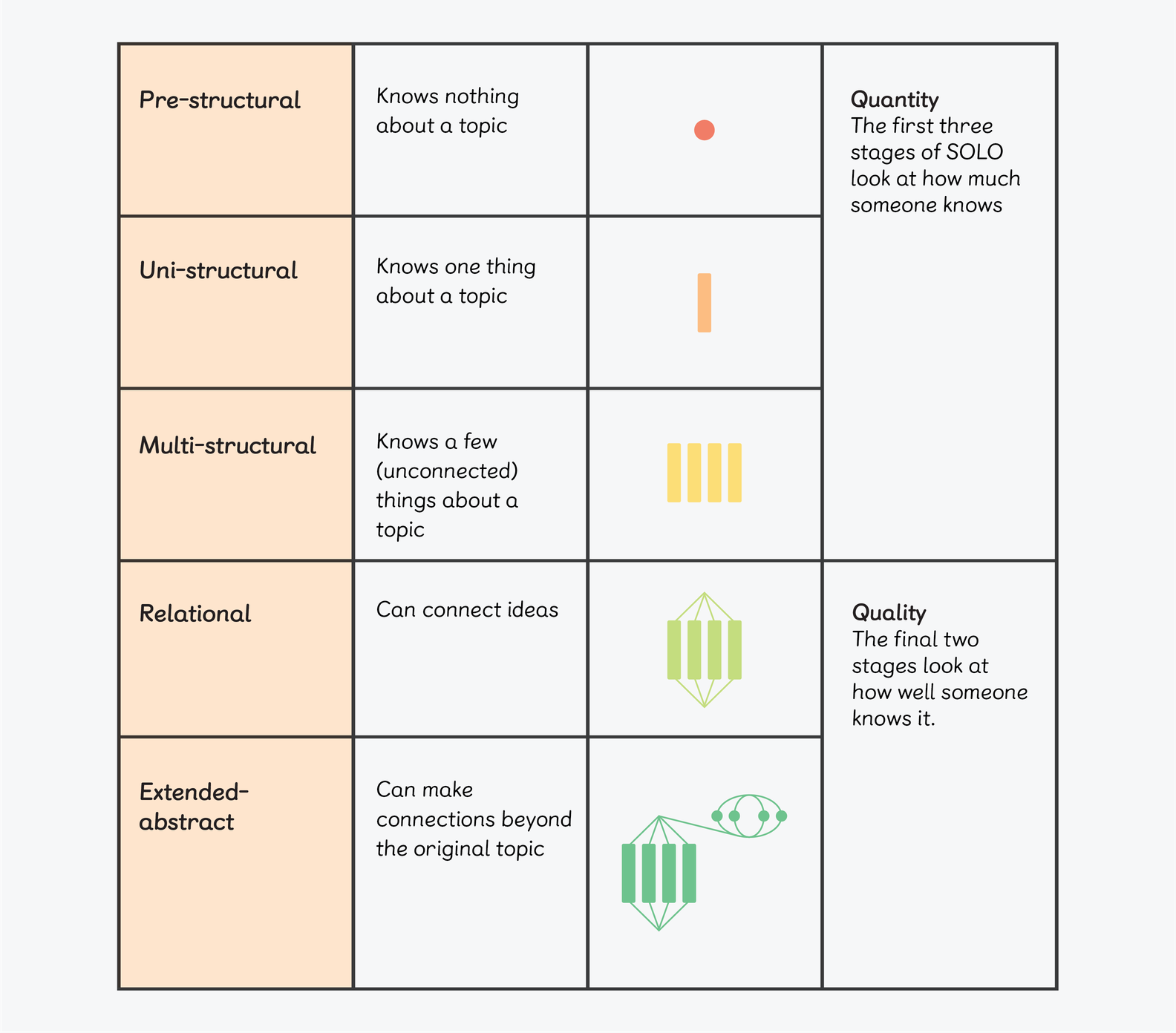
SOLO isn’t a hierarchy, but a series of stages. It suggests learning is a cycle rather than a linear process of steps, and learners can move to any part of the taxonomy, from the Quantity phase to the Quality phase and back again.

Every Maths — No Problem! lesson gives pupils the chance to play in the Quantity phase as well as in the Quality phase. An expert teacher knows when learners need to move between the two domains.

How do Maths — No Problem! lessons align with SOLO?

The structure of a typical Maths — No Problem! lesson could be described as:

• Present pupils with a problem to solve, known as the ‘In Focus,’ ‘Explore,’ or ‘Anchor’ task
• Ask pupils to find multiple ways to solve the problem (Polya)
• Give pupils ample processing time (Piaget) through collaborative working (Vygotsky)
• Take part in sense-making of the pupils’ methods, for example ‘Let’s Learn’ or ‘Master’ (Dienes and Skemp)
• Give pupils the opportunity to use their skills in smaller, guided groups
• Give individual pupils the opportunity to apply near and far transfer of their skills during independent work (Thorndike)
• Allow the pupils time to reflect on their learning through journaling to further develop their meta-cognition (Dewey, Flavell)

The first stage of the Maths — No Problem! approach is to present learners with the Explore or Anchor task, which invites pupils to move into the Quantity phase. Polya suggests solving a particular problem in many different ways. This takes pupils through the phases from Pre-structural to Uni-structural to Multi-structural.

‘Let’s Learn’ or ‘Master’ moves pupils toward the Relational phase. The greater the quantity of knowledge, the more complex the Relational phase may be. This complexity helps develop deeper levels of learning.

Here we ensure that the learning foundations become better bonded. Where pupils haven’t progressed to the Multi-structural phase, they are still given the opportunity to secure their Uni-structural understanding.

How does maths mastery help learners reach the Extended-abstract phase?

The move to the Extended-abstract phase looks at both the creation of new ideas and the familiar Concrete-Pictorial-Abstract (CPA) approach. The quality of Extended-abstract understanding depends on the quantity of knowledge and the ability to be creative.

The development of this understanding can be supported through the use of the Mind Challenge and My Maths Journal elements of the Maths — No Problem! textbooks. These not only help deepen the connections made in the main body of the lesson, but also give an opportunity to generalise the new ideas and concepts in an unfamiliar or novel setting.

By having mixed-ability groupings, you will sometimes see pupils who typically struggle to build knowledge show great ability in the connecting and extending aspects of the lesson.

As I often say, pupils learn when they learn, not just when we teach. And when pupils reflect on their learning, rather than on our teaching, an even greater amount of learning can take place.