How to use part–whole bar models in your classroom

Are you using bar modelling in your maths lessons? This visualisation tool is an essential maths mastery strategy. It supports the Concrete, Pictorial, Abstract (CPA) approach to learning.

All bar modelling starts with the part–whole model. These simple diagrams help learners make the jump from relying on concrete resources to thinking pictorially. Part–whole models are a great way for learners to make sense of a problem and decide which operation they need to use and why.

What is a part–whole bar model?

The part–whole model (sometimes called the part–part–whole model), is a simple pictorial representation of a problem that helps learners see the relationships between numbers.

A horizontal bar shows the ‘whole’ amount. Underneath it, an identical bar is divided into pieces to show the ‘parts’ of the whole. Here’s how to use a part–whole bar model to represent a simple addition question.

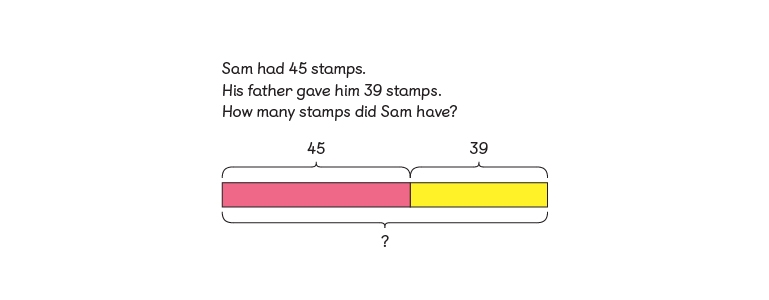
Part–whole bar models show that you know some information, but still need to find some information out. The bar can be split into as many parts as you need, depending on the amount of information you’ve been given. If the total is unknown, you might see the ‘whole’ bar replaced with brackets and a question mark.

Introducing part–whole bar models with your class

Maths lessons should always start with handling and exploring concrete items. Get your class to line objects up as they add and subtract with them. Make sure they can count with accuracy.

When your learners are ready to move on to visual representations, start by keeping one-to-one correspondence with connecting cubes. Learners should see that each cube is a representation of the physical object. Making each part a different colour helps children see that they’re different pieces of the whole.

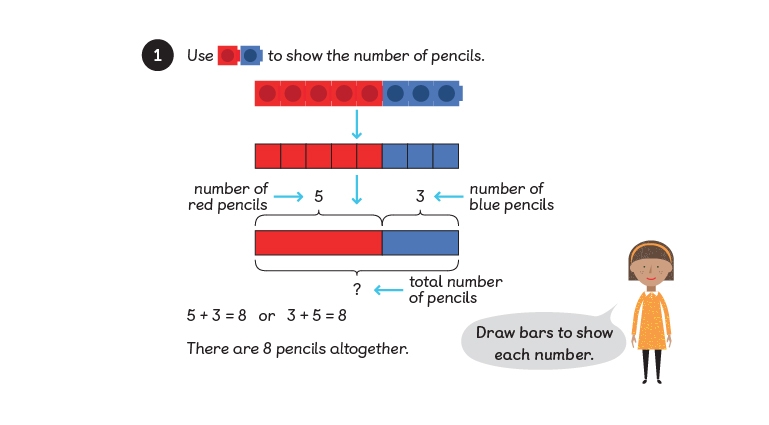
Next, show the equivalence of the parts to the whole bar. You could, for example, make a ten-cube bar just using red cubes. Or make another bar using eight blue cubes and two yellow ones. Now it’s easier to see that the two bars are equivalent to each other. You can rearrange the bars to make number sentences.

In time, you can draw a bar and display it alongside the cubes to help your learners to see a fully visual representation. Move away from one-to-one correspondence by working with larger amounts.

Learners will soon see that it’s far too cumbersome to use cubes or draw individual squares for a calculation like 25 + ? = 60. Ask them why you might use a smaller bar to represent a much larger amount.

Using part–whole bar models to solve problems

Problem solving is always going to be difficult for primary learners. Applying mathematical knowledge can be hard when learners don’t understand which operation they need to use. A part–whole model shows learners the problem in an accessible way.

Part–whole bar models are ideal for:

• Addition
• Subtraction
• Missing numbers
• Division
• Fractions
• Multiplication

They’re particularly useful for time and measurement problems as children often find these problems challenging.

Solving addition and subtraction problems

Part–whole bar models are a simple way to show word problems with a missing number element. Addition and subtraction questions are useful for demonstrating that you can break bars into unequal sizes.

Example addition questions:

• Tom buys a cake for 10p and a juice for 12p. How much did he spend altogether?
• I think of a number. I subtract eight from my number. Now I have seven. What number did I start with?
• Jenny scored 8.5 in a test. Ben scored 7, and Amy scored 15.5. What was their total score?

Example subtraction questions:

• What is the difference between 23 and 42?
• Dan buys 20 sweets. He’s eaten six of them. How many does he have left?
• Ellie has £14.50 to spend at the fair. She spends £4 on rides and £1.20 on candyfloss. How much does she have left?
• I cut 70 cm from a 3.4 m length of ribbon. How much is remaining?
• Sam bakes 320 cookies for the bake sale. He decorates 110 with chocolate buttons and 86 with icing. How many cookies are undecorated?

Solving multiplication and division problems

Learners need to know that a bar must be cut into equal parts when multiplying and dividing. Use a different colour to show any remainders.

Example multiplication questions:

• I put my socks into pairs. If I have eight pairs, how many socks do I have?
• Seven people each put five pens into a pot. How many pens are there in total?
• In the toy shop, 45 toys can fit inside one box. How many toys are there in five boxes?

Example division questions:

• There are 16 people in two equal-sized teams. How many are in each team?
• 65 children are going on a school trip. Each minibus can fit 11 children. How many minibuses will they need?
• Jenny shares 30 sweets equally between four friends. How many will each friend have? How many will be left over?

Visualising fractions and percentages problems

Part–whole bar models are perfect for visualising problems using fractions and percentages. Learners often find these hard to solve because they struggle to work out what the question is asking them to do.

Example questions:

• Which is larger, one-third of £123 or one-quarter of £168?
• Raj calculated 30% of 120. What answer does he get?
• A shop has a sale where everything has 20% off. I buy some shoes for £36. How much did they cost originally?
• Anya has a box of counters. One-third of them are yellow. One-quarter of the remaining counters are blue. The other 24 counters are green. How many counters does she have?

Moving on from bar modelling

Using bar modelling is a simple step towards algebra. Equations like 3a + 7 = 25 are easy for learners to visualise because they’re familiar with finding an unknown amount.

Bar models are useful, but they’re not the end goal — nor the only way to visualise word problems. Eventually, your class will move on from drawing out the bars but can always return to them if they need to. Use them as a bridge to move from concrete to abstract understanding.

Bar modelling is fast becoming the favourite approach for teaching problem solving. They’re easy to draw, simple to understand, and require no equipment. Plus, you can use them to tackle a huge range of maths questions.

Why not give it a try with your class? You could be surprised at the level of understanding your learners can demonstrate, just by using this simple visualisation tool.