6 magical maths activities to keep children engaged
Editor’s Note:
This is an updated version of a blog post published on August 25, 2017
The long summer holiday is the perfect opportunity to explore some of the more creative and magical ways to keep children engaged and focused on the fun of maths.
Looking for maths activities you can do with your children to keep them engaged in and excited over the summer? Here are a few of my favourite magical maths activities to entertain the whole family regardless of age or mathematical ability.
Build your own magic squares
Magic squares are fascinating. In a basic magic square, the rows, columns, and two diagonals all add up to the same number. This is called the magic number and in the illustration below, the magic number is 15.
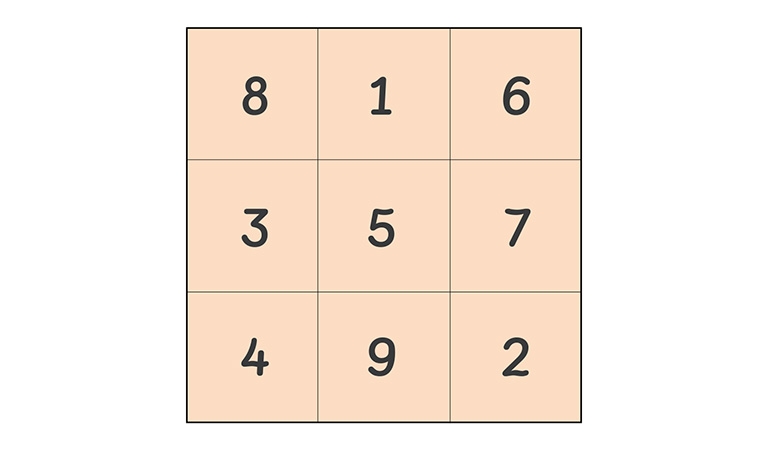
Sagrada Familia
One of my favourite magic squares can be found in Barcelona at the Sagrada Familia.
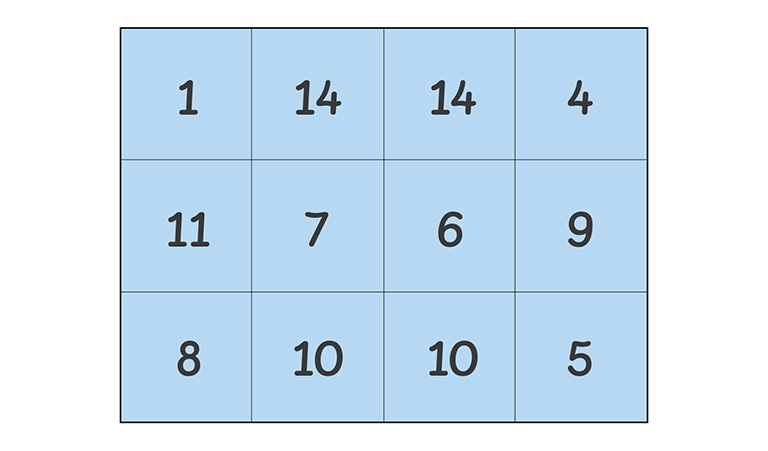
It also has many different patterns to explore. How many can you find?
The magic number here is 33. There are dozens of combinations of numbers that would produce a similar square, with numbers adding to 33. Can you find any?
How to construct a magic square
In the 19th century, Édouard Lucas devised the general formula for order 3 magic squares.
Consider the following table made up of numbers a, b and c:
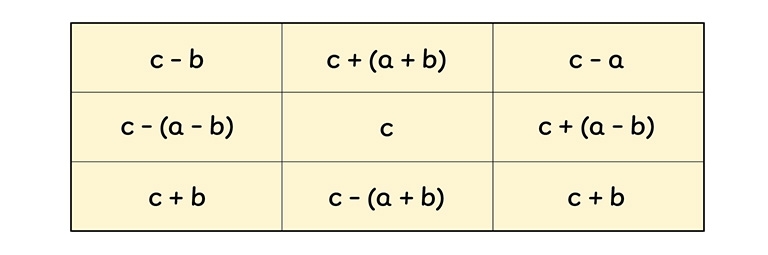
These numbers will form a magic square as long as:
- They are all larger than zero
- b must be larger than a
- b must not be the same value as 2 times a
- c-a must be bigger than both a and b
Explore the golden ratio
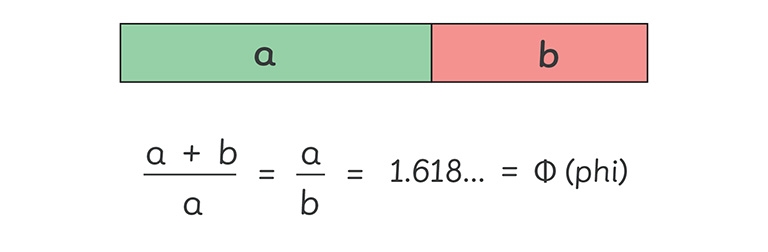
The golden ratio, denoted by the Greek symbol ‘phi’ is a special number in maths that is approximately equal to 1.618. It appears in architecture, art and geometry, and even in the human body.
The golden ratio is found by dividing a line into two unequal parts so that the whole length of the line divided by the longer part is equal to the longer part divided by the shorter part. Try exploring this yourself.
As humans, we like to see objects around us that are in the golden ratio, such as picture frames. The proportions of many buildings are also designed to be in the golden ratio. We are also designed in line with the golden ratio. Have a go at this activity from nrich.org.
Measure the following:
- Distance from the ground to your belly button
- Distance from your belly button to the top of your head
- Distance from the ground to your knees
- Distances A, B, and C
- Length of your hand
- Distance from your wrist to your elbow
Now calculate the following ratios:
- Distance from the ground to your belly button / Distance from your belly button to the top of your head
- Distance from the ground to your belly button / Distance from the ground to your knees
- Distance C / Distance B
- Distance B / Distance A
- Distance from your wrist to your elbow / Length of your hand
Write your results in the following table:
Can you see anything special about these ratios?
Be amazed by everlasting chocolate
Here’s a fun and magical maths activity. The everlasting chocolate trick appears to make a square of chocolate appear out of nowhere. Clearly, this is an attractive thought for the most reluctant mathematician. Here is a youtube clip that both illustrates and explains this phenomenon.
Try this time calculator
You may well be travelling over the summer, with children asking ‘Are we there yet?’ Maybe you have a car journey, followed by a train journey. How long will you be travelling altogether? You need magical maths activities. This method for adding periods of time may well dazzle your children!
For example, we have a car journey of 1 hour 35 minutes followed by a train journey of 2 hours and 55 minutes. To add two periods of time together, you just write the times as three digit numbers, add them and then add 40.
1 hr and 35 mins plus 2 hrs and 55 mins
Would be
135 + 255 + 40
= 430
4 hrs and 30 minutes!
Can you figure out why it works?
Figure out what happened
First, write down any three-digit number.
Multiply it by 13.
Multiply that answer by 7.
Now, multiply that answer by 11.
What do you notice? Does it always work? Why?
Make a Möbius strip
This is my all-time favourite activity to do with learners of any age and with the teachers that I work with too.
The Möbius strip is named after the mathematician August Möbius who invented the strip in 1858. It is curious because it only has one side and one edge. A Mobius strip is simple to construct. All you need is a long strip of paper, sticky tape, and a pair of scissors.
Take the long piece of paper and put the ends together as if you were making a headband. Before you attach the two ends with tape, give one of them a twist and then stick the ends together.
Now try drawing a line along the centre of the strip. What do you notice?
You will end up back where you started, without having to take your pen off the paper. So you have drawn on both sides of the strip of paper in one go, meaning that your original strip of paper, which had two sides, now only has one side!
Now cut along the line that you have drawn. What do you think might happen?
Try it and see!
There are many other interesting things that you can do with this strip. Try making another one, but this time instead of cutting along the middle, cut a third of the way from one edge. What do you think will happen this time?
Watch this video from Think Twice for more ideas:
Further Reading
Here are some books I’ve been able to take mathemagical inspiration from:
Can You Solve My Problems? by Alex Bellos
The Simpsons and Their Mathematical Secrets by Simon Singh
How Many Socks Make a Pair by Rob Eastaway
