The Importance of the CPA approach in the Early Years

Maths is an abstract concept; you could say it is like learning another language. Children in the Early Years need lots of practise and a range of different contexts to understand a mathematical concept.

Many educators have stated that the early years form the basis of a pupil’s mathematical understanding. These contexts also need to be appropriately linked to the children’s experiences. So how can we possibly accomplish this?

The Concrete-Pictorial-Abstract approach was developed in the 1960’s by Jerome Bruner. Bruner stated that children need scaffolding, with the use of manipulatives to understand such abstract concepts.

The CPA approach helps pupils to develop a deeper understanding of mathematical concepts. Without this, they may rely on rote learning. Rote learning will only allow pupils to imitate an adult’s methods in maths, which will result in them being unable to problem solve for themselves and transfer their understanding of mathematical concepts to new situations.

What does the CPA approach look like in the Early Years?

C is for Concrete

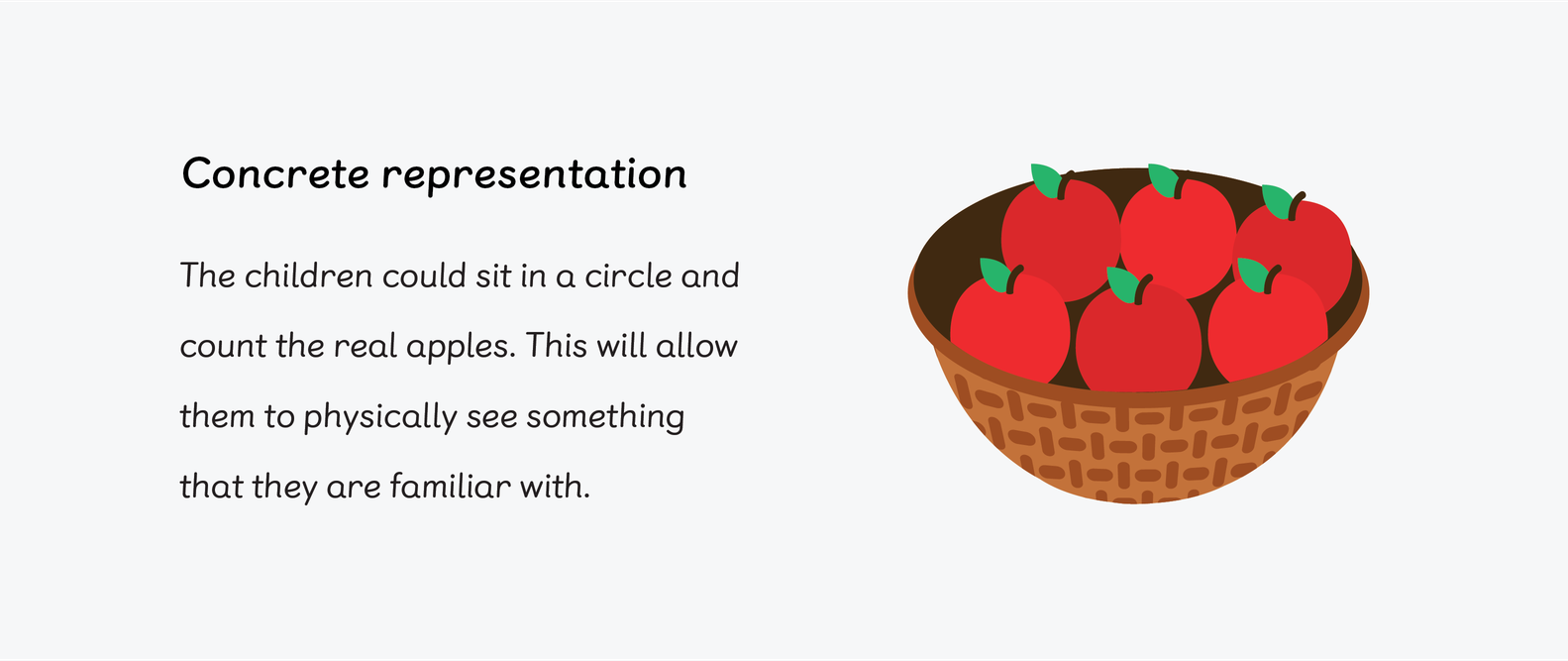
Children will use real-life objects to start with. Fruit is always a great, easy to get hold of resource in school! Younger children especially love a story to go with the objects as well. For example, I have a big apple tree in my garden and I love eating apples. Today I picked some apples from the tree and put them in a basket. Here’s my basket of apples. Can you help me count how many apples are in my basket?

The children could sit in a circle and count the real apples. This will allow them to physically see something that they are familiar with. This is classed as the concrete stage of the CPA approach which Bruner believed comes first for understanding.

Now that the children have touched and counted real apples — an object that is relevant to them is particularly important — they should be given many opportunities to practise this before you begin to introduce the pictorial stage.

P is for Pictorial

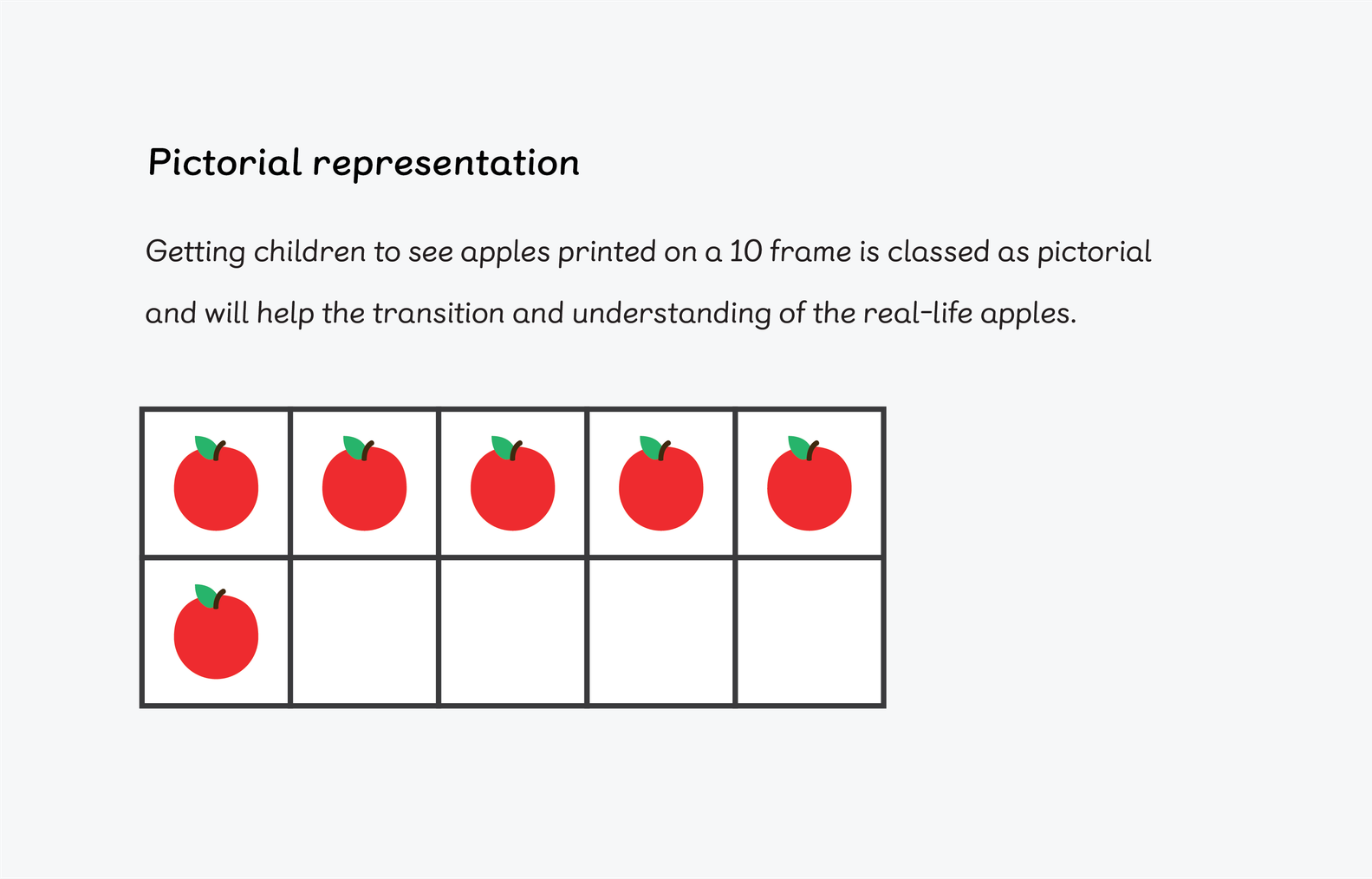
The pictorial part of the approach follows on from the concrete. Now that children have learned to confidently count various objects, you might go back to an experience like, for instance, apples. This time the children can physically place the real apples on a large 10 frame. They can see that the apples are still real, however, we have introduced a new concept — a 10 frame.

Once the children can do this, you could move them onto the pictorial method.

I always explain this part as the objects being ‘stuck’ on the page. We can’t pick the object up, we can’t move it about but we can still count them!

Getting children to see apples printed on a 10 frame is classed as pictorial. This helps children transition and understand that real-life apples are being represented.

The children will be able to progress towards more abstract representations because concrete objects have already been introduced. Leong acknowledges that the concrete to pictorial process is gradual.

A is for Abstract

Now that the children can count images on a page, they are ready for the complete abstract stage of the CPA approach. In this example, it’s the numbers. At this stage, the children should have already had many opportunities to count and understand the total of a range of quantities (to five or 10 objects).

They may use language such as ‘altogether’ or ‘in total’. Using this language throughout the process will contribute to their understanding of the abstract process.

The more the children see the number alongside the images, the more they will understand. What is six ? What does it look like? Can I touch and feel the quantity of it? Can I hold six objects in my hands? Now I know how to do that, I can count six objects on a page, and I know that six is the total of the set.

Pupils must use this prior knowledge to help them understand maths language and what it represents. Without the C and P of the CPA approach, pupils are at risk of not knowing what six is and just referring to it as ‘maths.’

Now that the abstract concept makes sense, children will be able to transfer their knowledge to solving problems. For instance, Erin said that eight is bigger than 10 because she could hold 10 sweets in her hand but couldn’t pick up the eight footballs. Is that right?

Leong explains that pictorial images and visualisation should be understood well enough for pupils to fall back on when needed to solve problems. If pupils know the CPA approach well enough, they will be able to make sense of this problem and visualise the 10 sweets and eight footballs. They should then conclude that despite being able to pick up 10 sweets, the quantity of sweets is more than the eight footballs.

Understanding what the CPA approach looks like in Early Years will help you make sure your pupils are on the right track to understanding mathematical concepts and gaining maths mastery.

References:

Aubrey, C., and Godfrey, R., (2003), ‘The development of children’s early numeracy through Key Stage 1’ in, British Educational Research Journal, Volume 29(6), pp., 821-840.

Aunio, P., and Niemivirta, M., (2010), Predicting children’s mathematical performance in grade one by early numeracy, in, Learning and Individual differences, 20, pp., 427-435.

Bloom, B. S. (1968), Learning for mastery. Evaluation Comment (UCLA-CSIEP), 1(2), pp., 1–12.

Haylock, D., and Cockburn, A., (2003), Understanding mathematics in the lower primary years. A guide for teachers of children 3–8, London: Paul Chapman.

Leong, Y. H., Ho, W. K., and Cheng, L. P., (2015), Concrete-Pictorial-Abstract: Surveying its origins and charting its future. The Mathematics Educator, 16(1), pp., 1-18.

Piaget, J., (1952), The child’s conception of Number. London: Routledge.

Wong, K., Lee, P., Kaur, B., Foong, P., and Ng, S., (2009), Mathematics education: The Singapore journey, Singapore: World Scientific Publishing.