Building fluency for the Year 4 Multiplication Tables Check

If you’re teaching Year 4, you’ll want to make sure your learners ace the online Multiplication Tables Check (MTC).

There are many websites and apps that replicate the MTC, but if learners don’t know their multiplication, testing isn’t going to teach them. Yes, if a learner has strategies to work out answers, practice tests will help them to get faster. But if they don’t have a way of recalling or calculating the necessary facts, no amount of testing will help them learn.

I’ve written previously about the importance of fluency and strategies to help learners become fluent. And that’s the key to preparing for the Multiplication Tables Check.

Do learners have gaps in their times tables understanding?

The first step is to establish which facts a child still needs to learn. The easiest way to do this is to give learners a blank multiplication grid and ask them to fill in as many facts as they can in five or six minutes. The gaps will tell you what you need to target.

If learners don’t have a secure understanding of multiplication facts, recalling their times tables is going to be as tricky as learning to recite a poem in an unknown foreign language.
So how can you help learners really understand multiplication facts?

Use matching cards with arrays

My favourite strategy to build fluency is to use matching cards, made with three cards — multiplication, product, array — in each set. Here’s a link to some printable example cards to get you started.

Using pre-made cards can help, but challenging learners to make their own cards is even more effective. Ask learners to make arrays from different objects and take photographs.

One of my former learners and his mum were shocked to discover how many arrays they could make from the baby’s dummies — they had no idea he had so many! A Year 1 boy I taught was delighted to discover his parents’ wine rack was an array and used his skip counting skills to calculate how many bottles of red wine they had. I’m not sure his parents were quite so delighted when he came into school to tell us all…

If a child struggles to make regular arrays, then either egg boxes or plastic meatball trays can be easy to organise. Stamper pens are also great for drawing arrays.

Use a multiplication square

Teaching learners how to put a multiplication square together is also valuable. I wonder how many times we assume that because we understand what it represents, they will too?

Can they identify square numbers as a diagonal line of reflective symmetry? Are they able to explain why the same facts appear on either side of the line? (The commutative law, or switcheroos as I’ve heard them called).

Can your learners use the distributive law to work out multiplication facts?

One of the most powerful activities I’ve done with a blank multiplication square is to show how you can use your 1, 2, 5 and 10 times tables to work out any other facts by using the distributive law.

If you know that 5 + 2 = 7, then you also know that (5 × 4) + (2 × 4) = 7 × 4. You could also work this out by using 10 – 3 = 7, so (10 × 4) – (3 × 4) = 7 × 4. Doubling patterns can also be used — if we know 2×, we can double this to get 4× and double it again to get 8×.

How many different ways can you and your learners work out each unknown fact from the things you do know? This activity is powerful because it gives children a way to work out a question if they can’t recall the answer. No longer are times tables either something you know or something you don’t — learners now have a way in.

Keep revisiting the blank multiplication square

Once learners can use reasoning strategies to complete a multiplication square, you can return to the initial activity of giving them a blank one to complete. How much can they fill in now?

It will be a big confidence boost for them to see how much more they know than they realised. You might choose to repeat this activity regularly, asking learners to record the time they take to complete the square each time so they can track their progress.

I’ve had learners who are so motivated by this that they ask for blank multiplication squares to take home to practice. If they become so proficient they can complete the square in under two minutes, jumble the numbers up so they have to move beyond relying on learnt patterns.

Commit the times tables to long-term memory

You want your learners’ long-term memories to be permanently changed. Daniel Willingham’s definition of memory as the residue of thought really resonates with me. So for learners to remember things, they need to think, or reason, about them.

Here’s a great activity to get learners thinking about their multiplication tables.

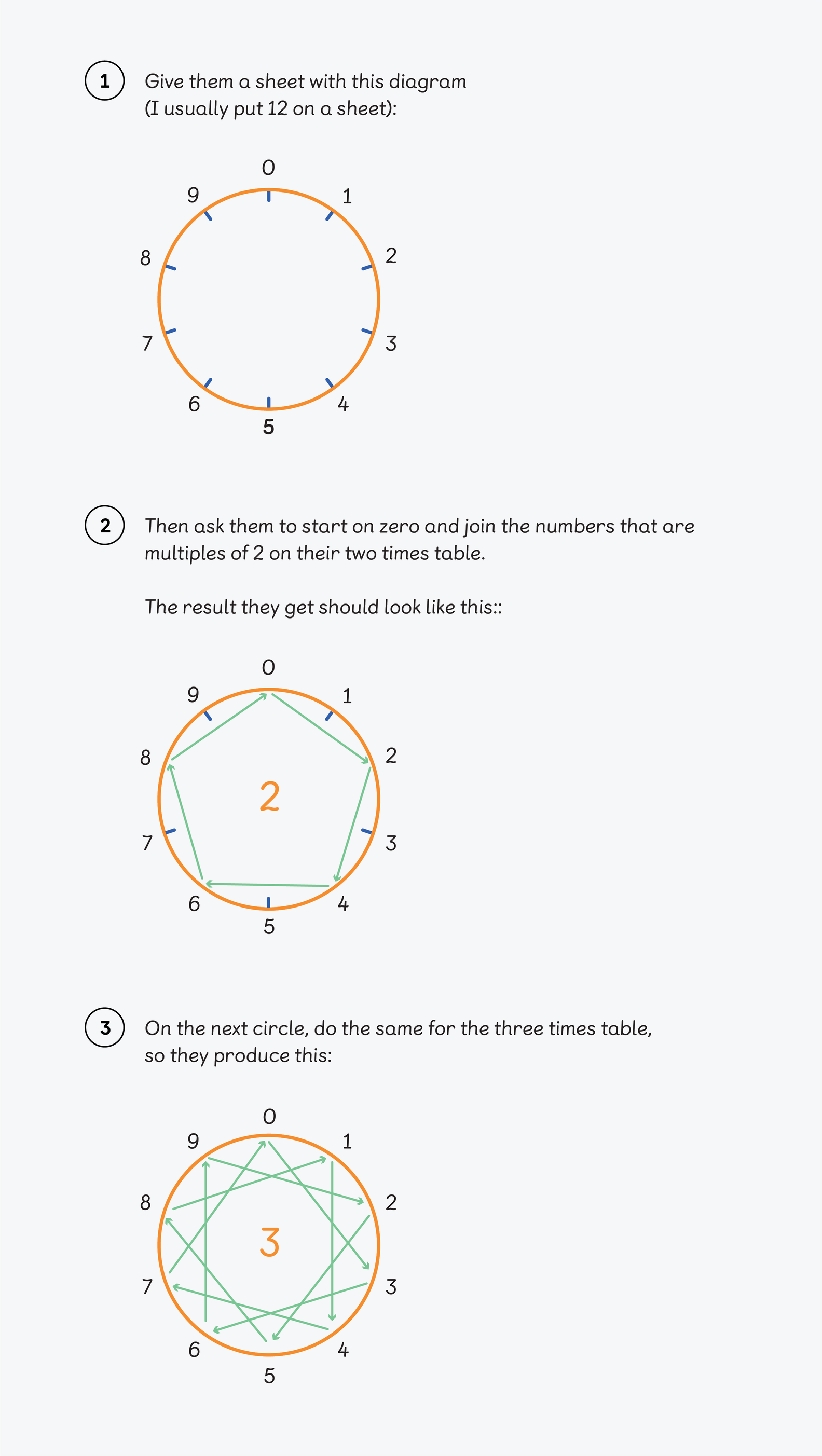
Once learners get the hang of it, ask them to do it for all numbers up to ten (or beyond). They will find that some numbers produce the same pattern. Which ones are these, and why are they the same? This can lead to great discussion and speculation. (Answer: the tables that produce the same pattern are number bonds to ten because we have a base-ten number system.)

Learners who understand how multiplication facts work and what they mean will have the confidence to practice their times tables, safe in the knowledge that they have strategies to work out facts they don’t know — yet.

References

Willingham, D. (2009). Why don’t students like school?: A Cognitive Scientist Answers Questions About How the Mind Works and What It Means for Your Classroom. San Francisco: Jossey-Bass.