Fluency Through Problem-Solving: It’s all connected
We often hear the word 'fluency' and think of speed. Quick recall, fast facts, answers that come without hesitation. But is that really what fluency means in mathematics? And if not, how do we help children develop something deeper, more meaningful and more lasting?
Fluency, in the way we understand it, goes far beyond memorisation. It’s about having a secure understanding of number and structure, and being able to apply that understanding flexibly and confidently in different situations. And crucially, we believe fluency develops best not through isolated drills, but through carefully structured problem-solving.
'Becoming fluent in the fundamentals of mathematics' is one of the three key aims of the English National Curriculum. But fluency doesn’t stand alone — it sits alongside reasoning and problem-solving as part of what it means to be mathematically proficient.
What is fluency really about?
The English National Curriculum defines fluency as:
…varied and frequent practice with increasingly complex problems over time, so that pupils develop conceptual understanding and the ability to recall and apply knowledge rapidly and accurately.
This definition gives us important clues. Fluency isn’t just about being fast. It’s about:
- Understanding not just remembering
- Flexibility not just accuracy
- Purposeful application not just rote procedure
So what does that look like in the classroom? And how can problem solving help us get there?
Building fluency over a lesson, a chapter, and over years
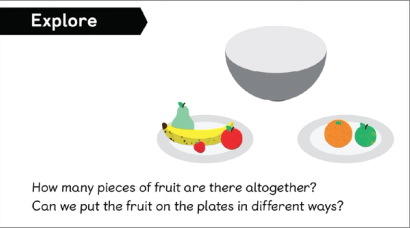
The Lesson
Fluency does not develop in a single moment. It builds gradually, with purpose, across lessons, chapters and years. Within a single lesson, pupils begin in the Explore, where they connect the new problem to prior learning and encounter a range of ideas. This phase gives children agency. They try things out, test ideas and begin to build understanding for themselves.
During the Master phase, the mathematical structure and strategies are drawn out, often highlighting methods pupils have already started to uncover. Rather than being shown a fixed process to remember, children are supported to analyse and make sense of methods, strengthening ownership and reducing the need for rote recall.
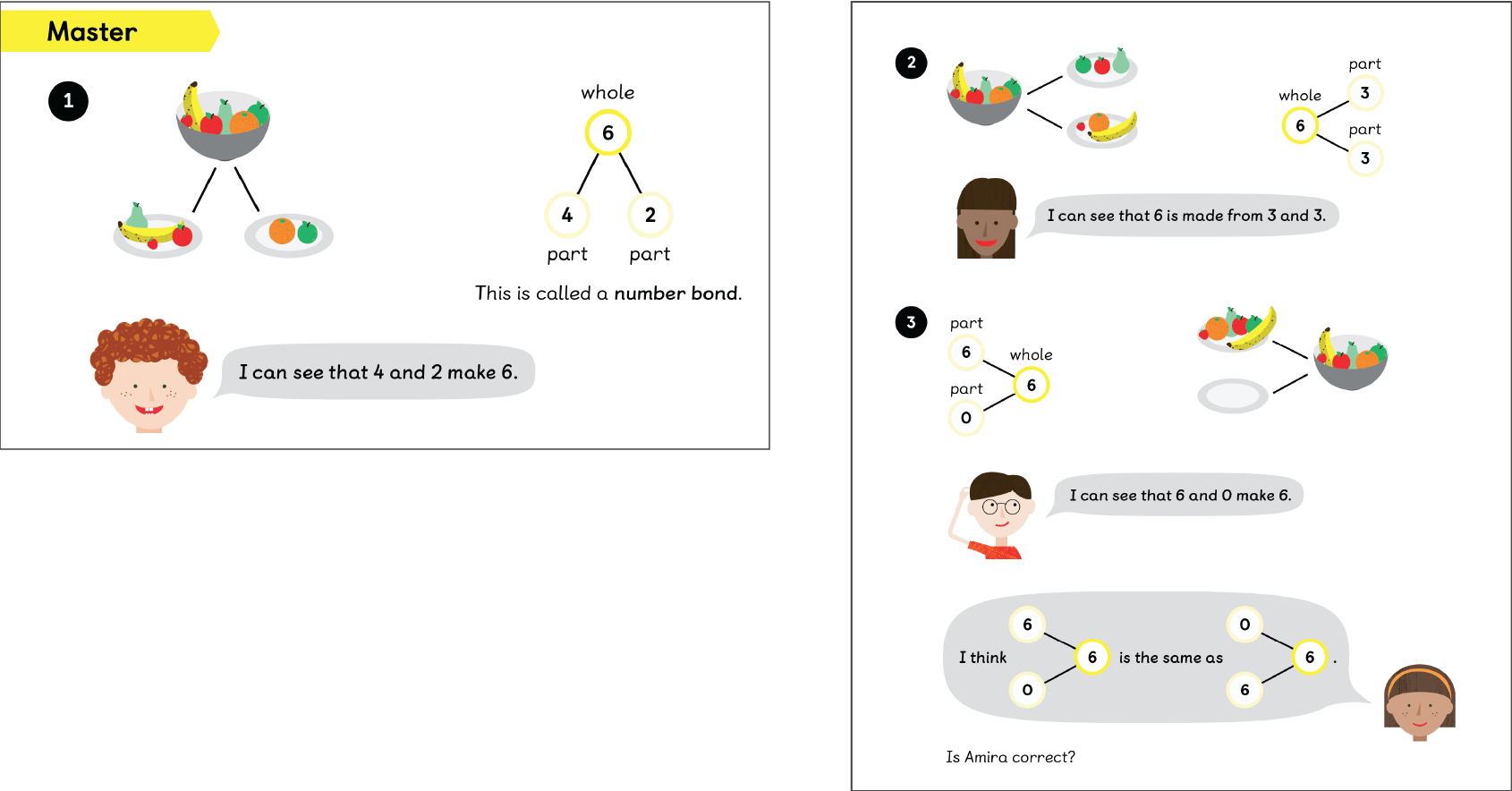
In Guided Practice, pupils are working on the maths rather than simply through exercises. They test ideas, refine strategies and make connections. Then in Independent Practice, they apply their understanding to new problems, embedding what they know more deeply through varied use.
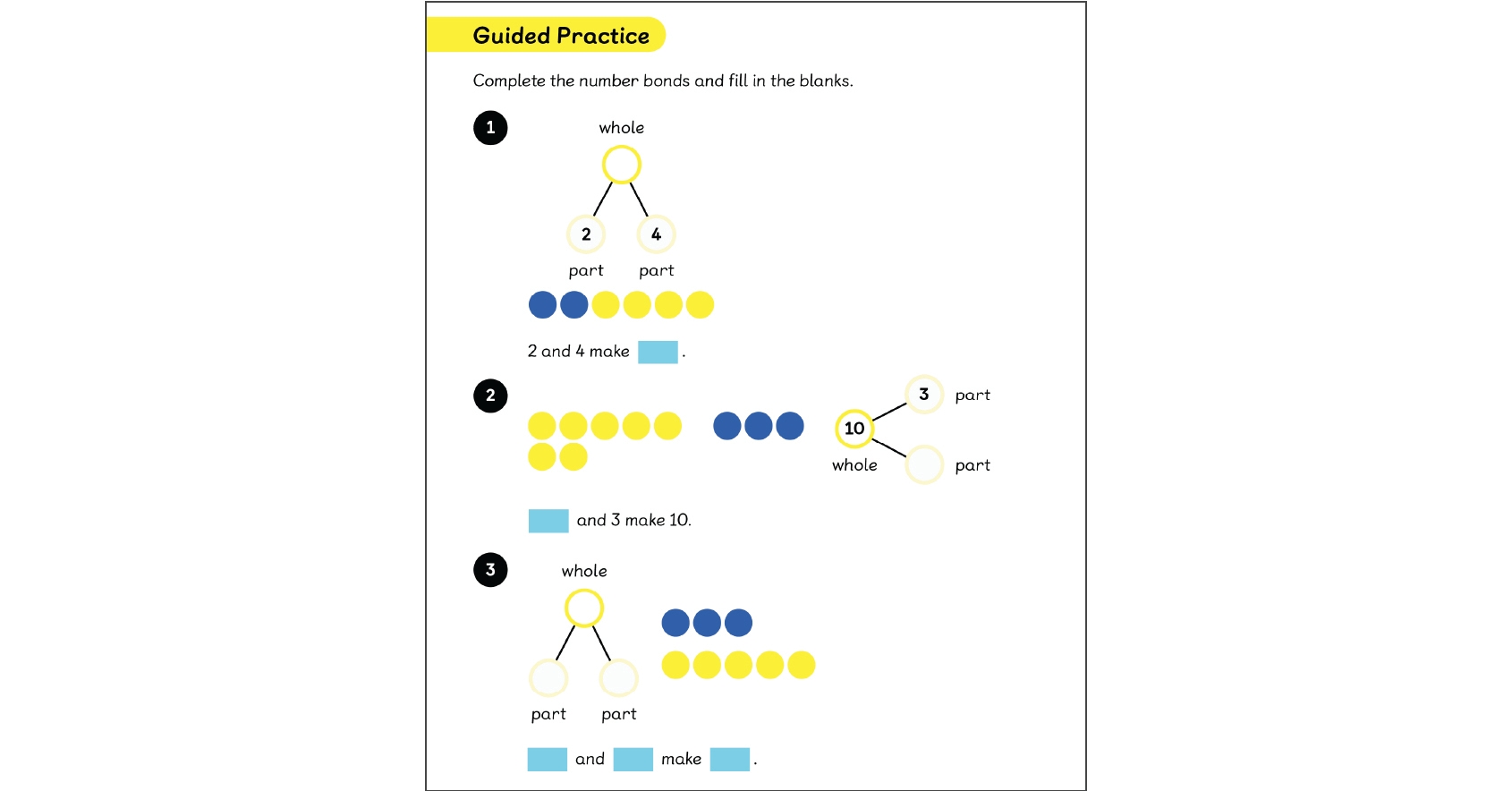
Over a chapter, these experiences accumulate. Ideas are revisited, extended and seen in different contexts. Pupils begin to choose strategies more confidently and reason about which methods are most efficient. Their fluency becomes more flexible and more robust.
Over years, this approach leads to sustainable learning. Children who understand what they are doing and why it works have less to memorise. They carry strategies with them because they have made them their own.
This progression supports fluency without reducing it to repetition. Each stage helps pupils connect ideas and strengthen strategies.
Transform Your Maths Assessment
Insights — our online assessment tool — gives you instant, powerful data to identify gaps and improve results.

Fluency as part of mathematical proficiency
Mathematical proficiency is described as consisting of five intertwined strands: conceptual understanding, procedural fluency, strategic competence, adaptive reasoning and productive disposition (Kilpatrick et al. 2001). This framework gives us a more complete picture of what it means to be successful in mathematics.
In this view, fluency is not isolated. It sits alongside and interacts with other elements of mathematical thinking:
- Conceptual understanding strengthens fluency because it helps pupils see why methods work.
- Strategic competence and adaptive reasoning grow as pupils make sense of problems and adapt strategies.
- A productive disposition encourages persistence, curiosity and a belief in one’s ability to reason and solve.
When pupils engage in problem solving, these strands develop together. Fluency becomes something dynamic — not just executing procedures, but choosing them thoughtfully, adapting them when needed and understanding why they work.
This framing reinforces our central point: fluency doesn’t stand apart from reasoning and problem-solving. It emerges through them.
Why fluency is misunderstood
Fluency is often misunderstood because it's commonly associated with speed and automatic recall. These are features of automaticity — the quick, effortless retrieval of facts like number bonds or times tables. In many classrooms, fluency has been equated with these surface-level indicators: fast answers and timed tasks.
But fluency goes further. In fact, when we look closely at what true fluency involves — choosing methods, adapting them, explaining reasoning and applying knowledge in unfamiliar contexts — we’re really describing problem-solving. And that brings us full circle: fluency doesn’t sit outside problem-solving. It grows from it.
How fluency and automaticity work together
Fluency and automaticity are closely linked, but they’re not the same. Understanding the difference helps us support both more effectively.
Automaticity refers to the quick, effortless recall of facts and procedures — things like number bonds, times tables or basic addition facts. It’s the kind of knowledge that doesn’t require deliberate thought, freeing up cognitive space for tackling more complex problems. Automaticity is helpful, but it isn’t the whole picture. Pupils also need to know when and how to use what they know. That’s where fluency comes in.
Automaticity | Fluency |
|---|---|
Fast recall of facts and procedures | Flexible, accurate and efficient application |
Enables fluency | Encompasses and goes beyond automaticity |
Often developed through repetition | Best developed in varied contexts |
Automaticity is part of fluency, but fluency also includes the ability to choose methods, adapt them and explain why they work.
Practical tips for teachers
Here are some ways to support fluency through problem-solving:
- Focus on strategies, not speed
- Ask: 'Who did it a different way?' or 'What made that strategy work well?'
- Use sentence stems like 'I know so I can…' and 'I chose this method because…'
- Encourage estimation: 'Roughly what do you expect the answer to be?'
- Make room for mistakes — they’re often where the best thinking happens
- Invite reflection: 'Which method was most efficient?' 'What would you do differently next time?'
Ask these questions often
- What strategy did you choose? Why?
- Did anyone solve it a different way?
- Which method was more efficient?
- Could this strategy work with different numbers?
- What does the bar model show you here?
- How is this like something we’ve done before?
It’s all connected
Fluency isn’t an add-on or an outcome of rote practice. It’s something we build over time by solving problems, exploring ideas and making connections. When we teach in this way, we’re not just developing fluent mathematicians — we’re developing thinkers.
Learn more
Building fluency through problem-solving
Reference
Kilpatrick, J., Swafford, J. and Findell, B. (Eds.) (2001). Adding It Up: Helping Children Learn Mathematics. Washington, DC: National Academy Press.
Louise Hoskyns-Staples
Rachel Walters

