Support maths mastery by exploring the three-part lesson

Well, you’ve come to the right place, we’re going to “pull apart” a Year Six lesson from the Maths — No Problem! textbooks and break down how it works in the classroom.

The lesson we’ve selected is from the Year 6A textbook (Chapter 2, Lesson 4 ‘Multiplying by 2 digit numbers,’ pages 38-40). We’ve chosen this lesson because it underpins a number of principles of the mastery approach, thoroughly illustrating the three-part lesson: the anchor task, guided practice and independent practice.

It gives pupils the opportunity to interact with and learn from one another. This lets them solve problems using a number of different methods they may not have previously known. On top of this, incorporating maths journaling into your lessons gives children the time and space to further develop their mathematical fluency and relational understanding.

The Anchor Task

Let’s start at the beginning. Our lesson opens with a potential real life problem called an anchor task. We read through it as a class and found that the calculation we needed to do was 23 x 113. The pupils then began to eagerly tackle the problem in pairs or threes using mini whiteboards. The main idea is to look for two methods of getting to the answer. If it was a clever day, there might even be three methods.

As the discussion flowed, we visited each group in turn, listened in on their conversations, asked them questions and encouraged them to explain their thinking. We didn’t show them a method or tell them if they were right or wrong. If they asked, we’d say we hadn’t yet worked it through. Concrete materials often come in handy here. For this problem some of the pairs used number discs alongside calculations.

After ten to fifteen minutes, the class found the following methods:

Method One: ‘The Dissecting Method’

The children often like to name their methods and this one was explained as follows:

“If you dissect (partition) the 23 into 10, 10 and 3, rather than multiply by 20, it us easier to multiply by 10. Once you have found that 113 X 10 = 1130, you then repeat it to get to 20. 113 X 3 could be similarly done with the hundreds, tens and ones multiplied separately. You then add them up to find the total amount of apples.”

Method Two: ‘The Standard Written Method’

The pupils found that there was a long way and a short way of tackling this calculation when using a written method. While the shorter method was familiar (from back in our own school days), the longer version showed the children’s relational understanding. In this version, they were able to demonstrate the value of each number that they were multiplying. They could also explain why we “put on a zero when multiplying by the 2” and why “the 3 was crossed out once we had finished multiplying with it.”

Method Three: ‘The Use What You Know Method’

Some children could also explain their method by telling the class: “having doubled 113 to find 226, you put on a zero because that’s what you did with the 2.”

We then tried to prove the calculation using smaller numbers: 4 x 2 = 8 and 4 x 20 = 80. 113 x 3 was worked out in two stages and the totals were then added together.

Each method told us the answer was that 23 boxes was enough for the 2500 apples. There would be 99 apples spare which, according to this year 6 class, could be used to make cider!

We drew the anchor task to a close by comparing our methods with those in the textbook. There was a different dissecting method – the textbook had split 113, we had split 23. The standard written form was there albeit with minor variations but our method three wasn’t included at all. This made the children feel really good about themselves!

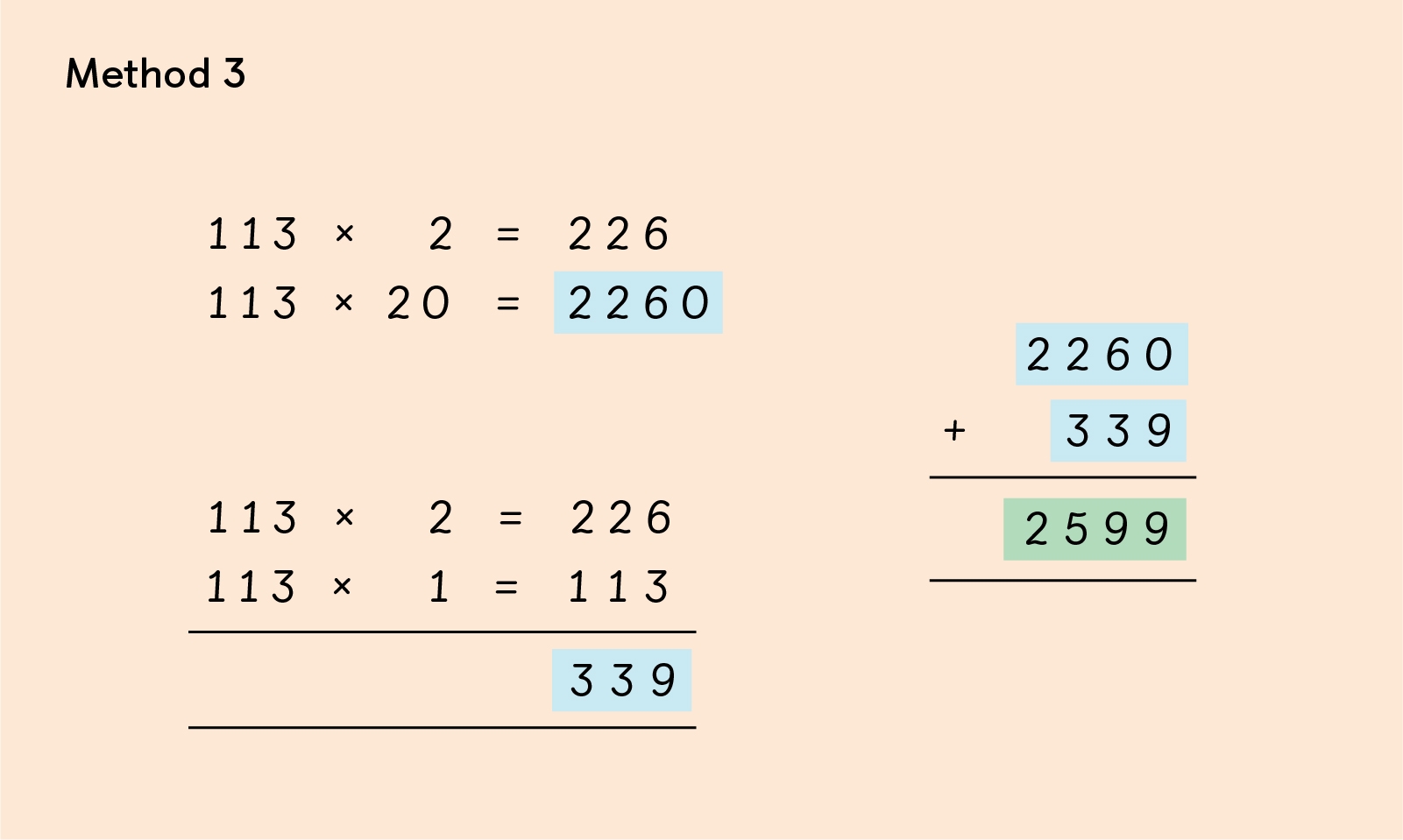
Guided Practice

With the methodology discussed, the children then used this learning in the Guided Practice section. Remaining in their pairs or threes, they worked through the problems together, continuing to talk to each other and share ideas.

The final two questions allowed the advanced learners to justify their placing of the digits — some could only feature in one place. The struggling learners tended to guess where the digits might go and then see if the sum worked out correctly. We are able to support these children by looking for any numbers we could definitely place whilst the former group explained their reasoning.

Independent Practice

For the final part of the lesson, children completed the independent practice section of the workbook individually. Having seen how the children have worked and interacted in the anchor task and the guided practice, it was easier to identify which children didn’t have a firm understanding of the problem. They could then be supported with our help and/or the use of concrete materials.

Initially, the workbook questions are scaffolded. As pupils work through them, the scaffolding is reduced and the questions gradually become more challenging. The ‘dissecting method’ is featured first, as the numbers can be accessed by the majority of the children. The final three questions are shown in the standard written method with the last question involving renaming as you have to add 9 + 2 in the tens column.

Extension

For our advanced learners, we provided a maths journal activity where children took one of the final three questions in the workbook and explained how they got their answer using any of the methods discussed today. They could either work individually in their maths journals or in small groups, creating a poster that could be referred to in future lessons. Inevitably, this work went beyond our allotted hour lesson but as this activity evolved through the discussion in the anchor task, we felt it was worth giving pupils some extra time.

None of the children opted for method three as their method of choice. In hindsight, we could have asked the children to write up the one they were least likely to use or facilitated a ‘lucky dip’ to make sure there was an equal spread. Even so, the work they produced really got ‘under the skin’ of how numbers are multiplied. The children learnt from each other and they all contributed in some way to the lesson.