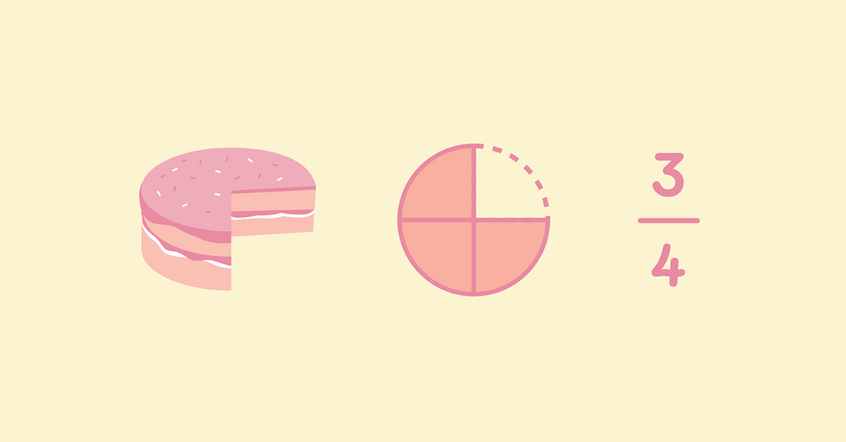How to teach fractions using the CPA approach

A few years ago, I was fortunate enough to attend a professional development course taught by Dr Yeap Ban Har. He explained that one of the major reasons children struggle with conceptually understanding fractions simply comes down to the way we write them.

And yet, the importance of recording fractions in a way that’s easy for children to understand is fundamental to teaching maths for mastery.

Perhaps sharing his advice can help you and your teaching practice too.

Why difficulties can arise from the way we record fractions

One of the major difficulties when it comes to understanding fractions is the convention of how we record the information.

To unpick this, one of the first things we need to understand is that, in mathematics, there are four kinds of numbers:

1. Cardinal Numbers
   Cardinal numbers denote a quantity: 1, 2, 3, 4, 5.
2. Ordinal Numbers
   Ordinal numbers define the position of something in a series: first, second, third.
3. Measurement Numbers
   Measurement numbers have a unit attached to them. Saying “I weigh 50,” doesn’t make sense; we need to include a unit of measurement, like “I weigh 50 kgs.”
4. Nominal Numbers
   A nominal number is a number used only as a name. For example, the 23 bus.

Why is knowing this important when teaching fractions?

If I asked you to write ‘3 quarters’ on your paper, most of us would likely write the symbolic notation ³⁄₄ to represent the fraction. As you can see, this means we would write the numerical symbol 3 to represent the numerator, and the numerical symbol 4 to represent the denominator

However, the way we record the denominator so similarly to the numerator can cause issues for many learners.

When we record the numerator, we use a numerical symbol (so, a number) in a cardinal way to represent the quantity. When we record the denominator, we also use a numerical symbol, but we’re using it in a nominal way. By representing the denominator with a numerical symbol, many learners assume it is also a cardinal number like the numerator, when in fact it is not. The denominator is essentially a noun — it’s the name of the fraction.

For example, saying ³⁄₄ is the same as saying ‘3 apples’. What we mean is ‘I have 3 of something. I have 3 of that thing. I have 3 quarters.’

Children often struggle when we’re teaching them how to record fractions, because we don’t explicitly teach them that the denominator is not a cardinal number — it’s a nominal number.

What’s the most common mistake children make when learning fractions?

This lack of understanding the difference between the numerator and denominator is illustrated when learners begin adding fractions. The most common mistake children make is that they will add the denominators together the same way they add the numerators. This reflects a lack of understanding that the denominator is a noun — it’s the name of the fraction — and not a quantity, like the numerator.

Key takeaway: We need to give learners an understanding that the denominator and the numerator are different, even though we are representing them both in the same way.

Easy ways to help learners understand and record fractions

The symbolic notation of fractions can create problems for learners. And often, as teachers, we introduce it too early, which unintentionally creates further confusion. So how do we help children develop an understanding that the denominator and the numerator are different?

Here are some easy ways to teach fractions and give your learners a deep understanding of how they work.

1. Use concrete resources

Concrete resources are critical for giving learners a conceptual understanding of fractions. Using resources to support teaching the concept of adding fractions is an easy way to record fractions and help children see that only the numerator is cardinal and represents a quantity.

2. Don’t introduce the concept of fractions with the symbolic notation

Fractions follow the language convention of ‘number plus noun’, like place value. For example, ³⁄₄ follows the same language convention as ‘3 tens.’ Both mean ‘we have 3 of that thing.’

When we introduce fractions to younger learners, explicitly following this convention will develop their understanding of the numerator and denominator. Rather than recording fractions with the symbolic notation, record the numerator with the numerical symbol and the denominator as a written word.

For example: ³⁄₄ can be recorded as ‘3 quarters’.

Recording fractions initially as ‘the number plus the noun’ will help learners develop an understanding that the numerator is cardinal and the denominator is nominal.

3. Use pictorial and visual representations to support abstract maths.

Similar to using concrete resources, it’s important to support abstract maths with visual representations. Drawing diagrams to represent ³⁄₄ added together with ²⁄₄ will help learners develop an understanding that only the numerator represents a quantity.

Visually representing the abstract concept of fractions is important for developing your learners’ conceptual understanding of fractions throughout their primary school learning. Visual representations will help learners understand conceptually what the abstract notations and procedures mean.

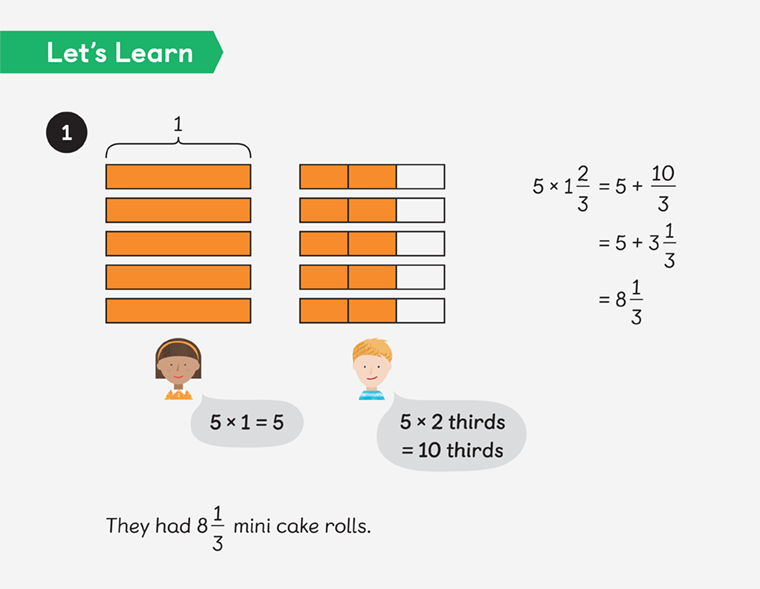
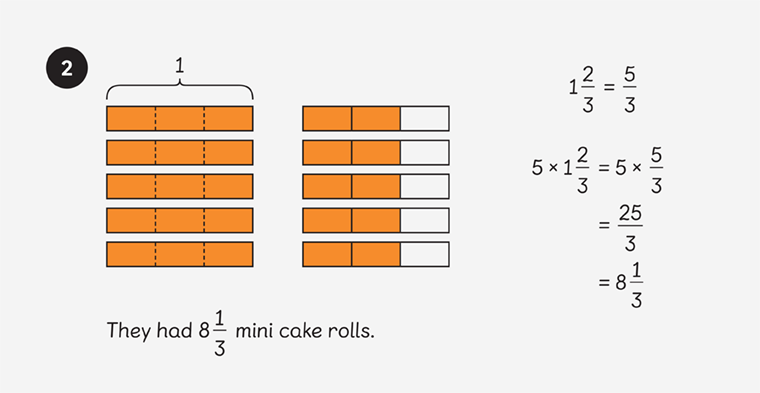
Information in mathematics is highly encoded — really, we’re using a bunch of symbols to represent abstract concepts. So to ensure we give our learners a conceptual understanding of fractions, we need to carefully consider how we’re presenting the information to them.