How can a spiral curriculum support you and your learners?
Ever heard of Jerome Bruner’s spiral curriculum model? This carefully-crafted teaching approach seems practically made for this unusual era of disrupted learning.
The Maths — No Problem! Primary Series is designed using a spiral curriculum, where every textbook and lesson builds upon the learning that came before. Daily lessons cover required curriculum content and revisit prior concepts to encourage essential learning connections.
Learn how a spiral curriculum can support you and your learners, and why this curriculum works so well for children who may have missed out during lockdown.
What is a spiral curriculum?
In the 1960s, Jerome Bruner outlined an educational approach where learners revisited the same topics, each time deepening their understanding. This approach is known as a spiral curriculum model. Knowing what’s involved in a spiral curriculum allows us to plan for our learners, and knowing how this curriculum works can help.
Bruner recognised the benefits of certain features of a spiral curriculum:
- Topics are revisited to consolidate understanding
- Topics increase in complexity
- New learning is related to previous learning
- Learners’ mathematical understanding increases
Where can you see the spiral curriculum in Maths — No Problem! textbooks?
The spiral curriculum is built into the Maths — No Problem! teaching approach. It’s an intuitive, consistent lesson structure that saves time needed for lesson prep, and gives you peace of mind that concepts are being revisited and reinforced.
Here’s how it works.
1. Topics are revisited to consolidate understanding
Throughout the Maths — No Problem! Primary Series, learners revise topics and ideas on a number of occasions throughout chapters and year groups.
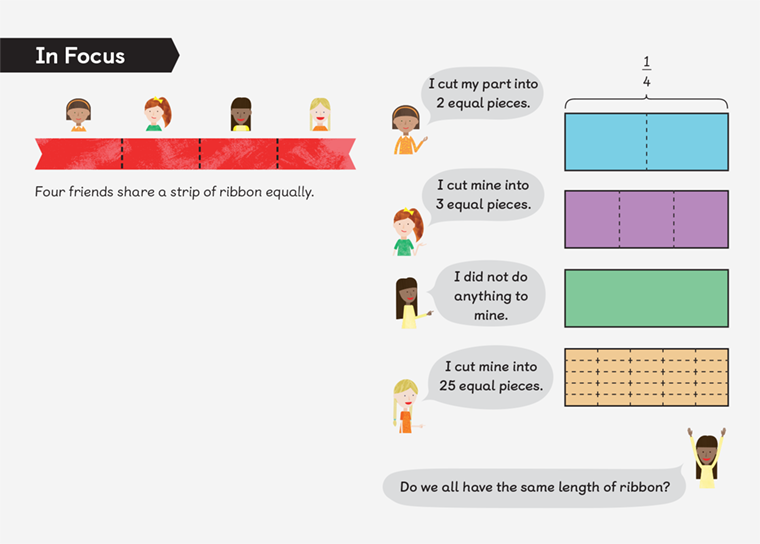
The books ensure that children are guided, step by step, through a series of ideas in a structured and sequenced way. In this example we can see how the development of fractions progresses through the years.
In these Year 1 to Year 6 examples, you can see certain features that encourage children to access new learning. In the initial lessons of the chapter, all examples are using rectangles and squares. This allows learners to use easily available materials like paper to model these situations. You’ll also see that if the prior learning is not secure, there is an opportunity to revisit these ideas without having to provide a completely separate lesson. There is also reinforcement of the language the children have been developing over the years.

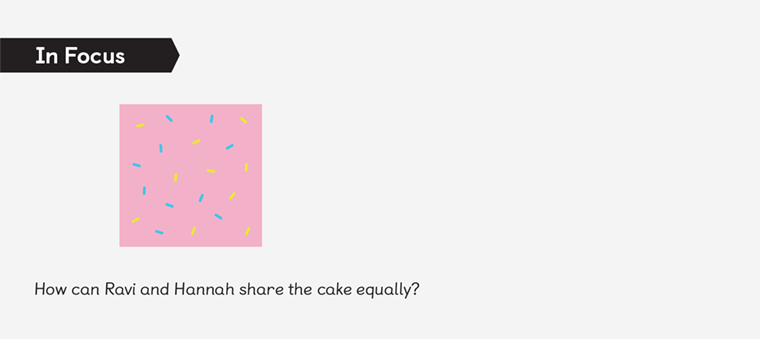



2. Topics increase in complexity
A spiral curriculum needs to continually build on the new ideas children have learned. In order to do this, the level of difficulty and complexity needs to increase until that idea is mastered. You can see how this is developed by looking at the lesson titles from the Maths — No Problem! Textbook 4A, Chapter 2.
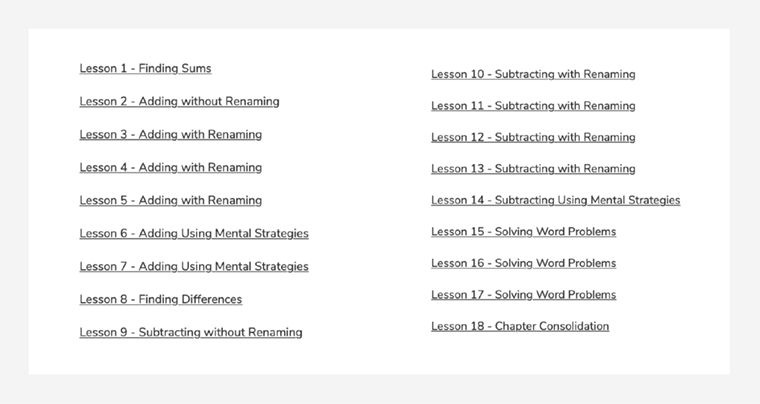
In Lesson 1, learners revisit the previous year’s objective, giving the teacher an opportunity to assess the prerequisite knowledge for the chapter, but also so children can remind themselves of what they have already learned.
In Lesson 2, learners are introduced to adding numbers that are larger than what they’ve previously used, but without having to rename. This allows children to attend to the new idea being developed. You’ll see that because it’s a skill they’ve practiced many times, it’s likely they will understand this idea in a relatively short time. That is why there is only a single lesson on this topic.
Lessons 3 to 5 build on the previous lessons, but now include renaming. This is a more complex skill, particularly as there are more numbers that may require renaming than learners have previously experienced.
In Lessons 6 and 7, the process moves to mental methods where learners need to visualise the problem and associated calculation. The complexity in Lessons 6 and 7 increases as there are not the same visual prompts we find in a written method. In order to manage the mental process, the number of aspects the learner needs to attend to to solve the problem must decrease. This, however, has been carefully managed and supported in the previous lessons.
Boost Your Practice with FREE CPD
Receive a CPD boost every time you refer a school! Both you and the referred school will earn a full day of CPD and 2 free places on our 3-day Essentials of Teaching Maths Mastery course (valued at £1700).
Get started on helping struggling schools reach maths success now!

3. New learning is related to previous learning
As the children develop, practice and embed their understanding of a new idea, they no longer have to attend to that particular part of their work. They are ready to learn something new, now that they have a prerequisite knowledge to learn it. In the examples below, we can see two levels of variation that are needed to have an effective spiral curriculum.
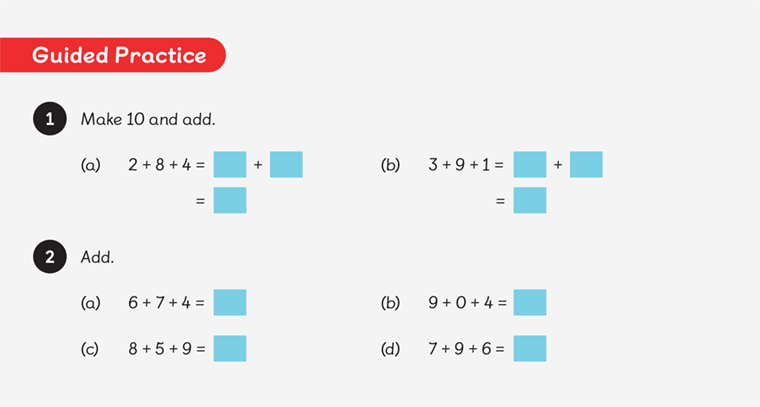
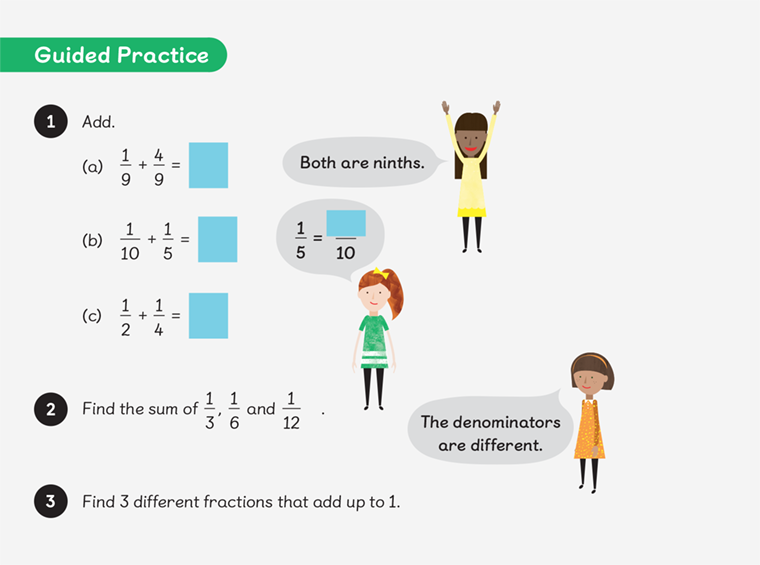
In the first instance, we can see the variation between the questions supporting the children to use a ‘making ten’ strategy, with questions of increasing complexity. However, the step before this was crucial. The example used pots of flowers: children learn that they can only add the same thing, using the same noun. The ability to do this starts in the early years when they may see one boy and one girl but two children. This idea is further developed, as we can see in the next example. Lulu reminds us that the denominators are both ninths — they are the same noun, which allows a learner to carry out the addition calculation with the same simplicity as if they were adding one apple to four apples. The concept of adding parts is new and provides an increasing level of difficulty, but the ideas that were developed earlier allow children access to the new learning.
4. Learners’ mathematical understanding increases
Another key aspect of a mastery approach is that everyone can learn. If a learner starts at the right place and is given the right amount of time, they are capable of learning anything. If we approach our lessons with this in mind, we need to be ready to respond to a child’s changing understanding of new ideas. Their ability will change as new ideas are understood and practiced. This is true of everyone. We may have the ability to make a cake, but not the ability to make a three-tiered wedding cake. We’re not saying that we lack the inherent ability to do so, we just haven’t developed the ability to make such a cake yet. But if we choose to, there are many skills we need to learn and much practice we need to undertake, often under the guidance of an expert. And we need to be prepared to put the effort in to learn.
How does a spiral curriculum support you and your learners today?
A huge amount of thought goes into designing a spiral curriculum. Not only do the lessons need to support new learning, but we also need an opportunity to further practice and develop ideas that may not have been learned the first time around. We also need to ensure that key skills are embedded throughout the curriculum.
When schooling is disrupted, as the world has experienced, the importance of a spiral approach to the curriculum cannot be understated. Understanding the elements of a spiral curriculum helps us adjust to meet the needs of our learners. We can also feel reassured that the key themes and topics will be revisited and in turn lead to deeper understanding.

