Asking effective questions gives you information you need to move learning forward. Improve your questioning skills in the classroom by focusing on three key areas: assessment, support and challenge.
Classrooms are full of questions. From children, teachers, school visitors, other staff, parents — the list goes on. We use questions to gather information to use in a variety of ways. But are there ways to improve our questioning skills over time?
Improving your questioning skills starts by looking at the objective of the question you’re asking. It can also be helpful to break it down into three different areas of questioning: assessment, support and challenge.
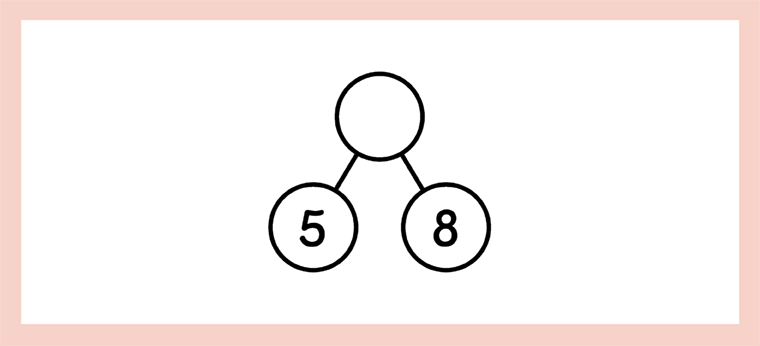
With that in mind, let’s look at some effective questions you can use for the following equation:
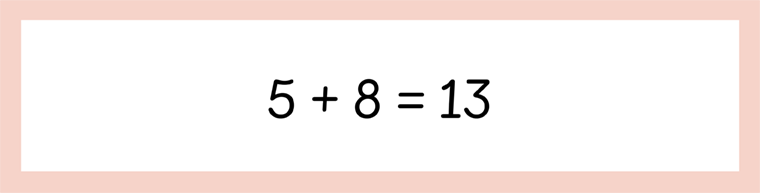
Effective questioning for assessment
Effective questioning for assessment helps you find out what a learner knows in the most efficient way possible. You can develop questioning for assessment as long as you have a detailed understanding of what a learner might do to understand and solve a maths problem.
To assess accurately, you should think about how the ideas needed to solve 5 + 8 = 13 have developed and develop questioning accordingly.
Can they read the symbols?
While pointing to 5 in the equation, ask questions like:
What is this?
What is the name of this?
Can you see five anywhere else in the classroom?
Can you make five for me using counters?
Can they represent the problem?
The next thing to look at is how well your learners can represent the problem. Ask them questions like:
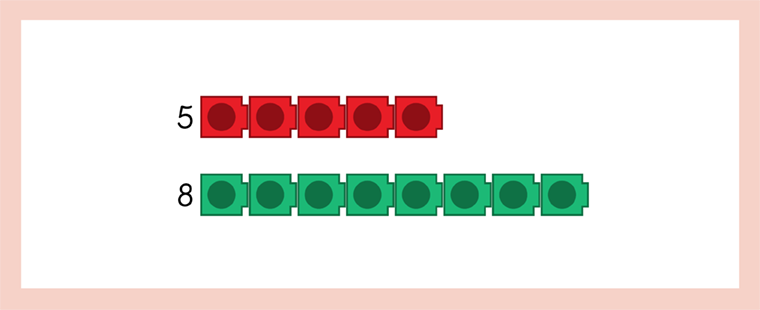
Can you make this problem using concrete materials? (counters, cubes, blocks)
Explain to me what this means. What do you have to do?
Can you imagine five things and three things?
What would bring them together?
Is it possible to draw a picture to show this question?
Do they have the prerequisite knowledge?
Assessing for prerequisite knowledge will help you determine the level your learners are at. The following questions can be useful for this equation:
Can you start counting from 5? I will tell you when to stop.
Can you start counting from 8? I will tell you when to stop.
Can you start counting from 1? I will tell you when to stop.
Can you get 5 counters for me?
Can you get 8 counters for me?
Can you count all of the counters?
Can they use the part–whole strategy?
The part–whole strategy helps learners visualise the relationships between numbers. These questions can determine whether your learners’ grasped the concept or not:
Someone has said making ten helps, what do they mean?
Can you use ten frames to help you solve this problem?
Eight and what makes ten? Five and what makes ten?
How does knowing this allow us to make ten here?
Can they reason and apply known facts to a similar question?
Reasoning skills are the key to facing more complex maths problems in later school years. For this equation you can ask your learners:
How does knowing 5 + 5 help us answer 5 + 8?
How does knowing 8 + 2 help us with 5 + 8?
If I know 8 and 8 makes 16, how can that help us with 5 and 8?
Effective questioning for support
Children tend to stop learning for two reasons: they are not sure what to do, or they already know it.
Effective questioning for support is a vital tool in supporting children who might be struggling with an idea or calculation. Even though direct instruction is important in children’s learning, we can pose questions that support children to continue learning.
So for an equation like 5 + 8 = 13, you can ask the following questions.
Can you model the problem?
Can you show me the problem using concrete materials? Always be aware that materials need to be appropriate to the problem. For this particular problem, ten frames work nicely.
Can you model this part of the problem?
Breaking up the problem can allow a learner to not only access the problem again, but it also allows them to attend to small parts that are manageable and make the bigger idea easier to learn.
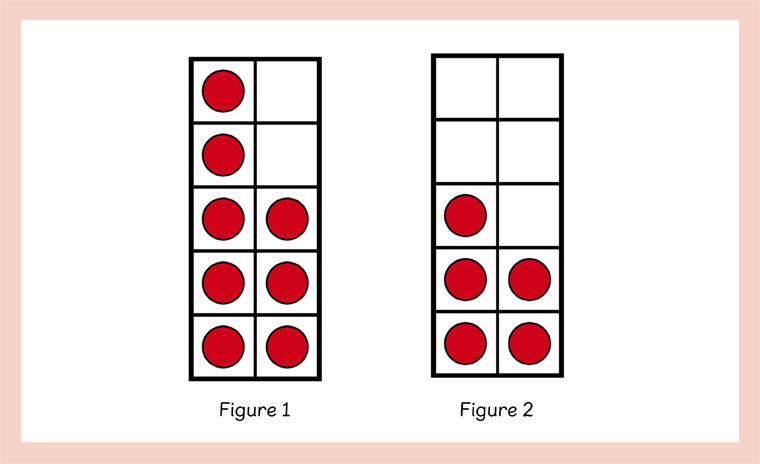
In this case the learner could make 8 on a ten frame to see that it can be arranged as 5 and 3 (Figure 1). Or you could ask the learner to make 5 in a pairwise arrangement so they can see 5 as 3 and 2 (Figure 2).
What do you notice?
This is a great example of effective questioning for support as there may be a number of aspects a child could notice. For example, if we ask them to make the problem using ten frames, we can draw attention to the gaps in the ten frame as well as the counters. They may notice there are only two gaps in one ten frame.
Is that the first frame to fill? They may notice that questions that involve making ten always have enough counters to fill one ten frame.
We could also ask what they notice about the answer. In this instance, an odd number and an even number make an odd total. What do they notice about two evens? What about two odds? This pattern spotting is not only important to maths but also provides valuable practice while the investigation takes place.
Effective questioning for challenge
When children need a challenge that’s based on the idea they’re learning, you can use effective questioning to help provide that.
There are many occasions when small initial changes result in final, large conceptual changes. Ensuring you understand the effect of any change to the problem can help manage differentiation and help support children’s learning, no matter which stage they are at.
So, back to our original equation: 5 + 8 = 13
Here are the effective questions for challenge that are sure to stretch your learners and encourage deeper mathematical thinking in your classroom.
How can the problem be changed?
What would happen if you changed the numbers in the problem? (One-digit for one-digit, two-digit for two-digit.)
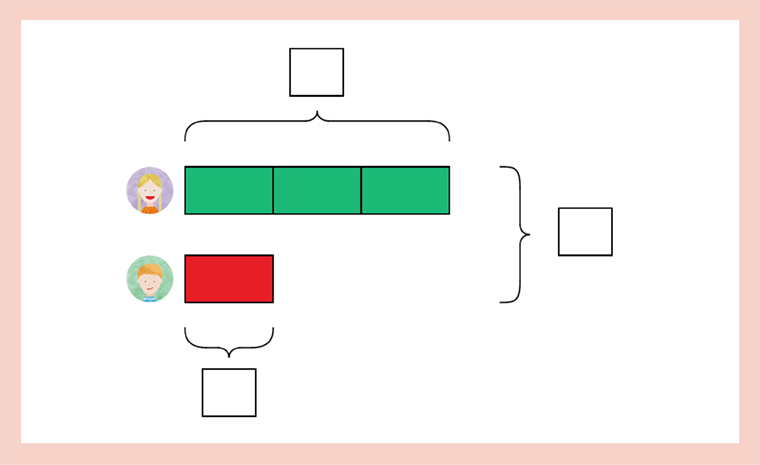
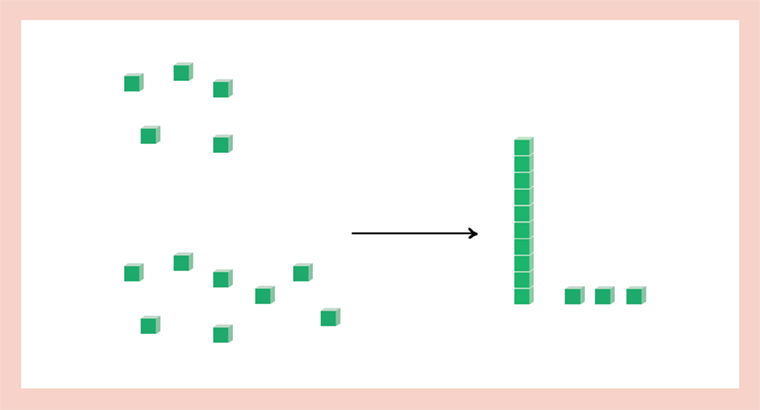
If I find one solution, is it possible to find other information? (See Figure 3.)
Figure 3
Can you write your own similar problem?
Does the context work with the numbers you have chosen?
How does the change you have made affect the outcome?
Once you have changed one part of the problem, can you describe how this changes other parts of the problem?
Why do the other parts change?
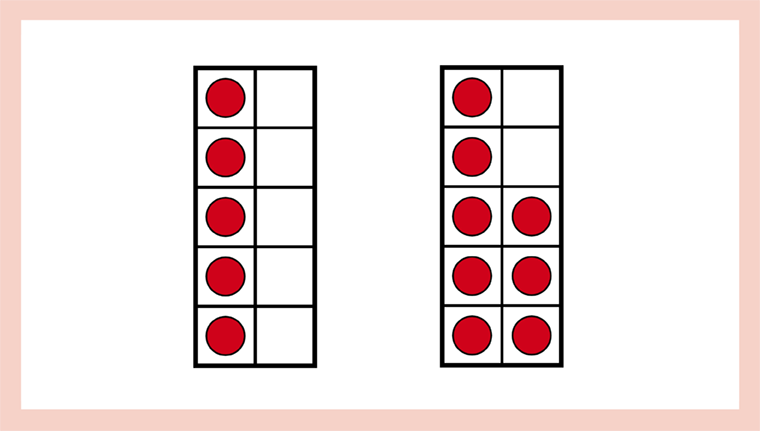
Can you write a problem for these representations?
The representations can be organised however you like. They don’t need to be labelled as they all relate to the first question.
Can you describe what is different and what is the same about these representations?
The key to effective questioning is thorough planning and sound subject knowledge. While there is an infinite number of questions that could be asked relating to 5 + 8 = 13, these examples help us see that effective questioning not only helps us become more effective teachers. It also provides the opportunity for children to become effective learners.
