Making the most of bar modelling
Editor’s Note:
This is an updated version of a blog post published on May 15, 2019.
How do you knock a teacher’s socks off? Show them a game-changing technique that helps children solve even the trickiest mathematical problems. It’s called bar modelling and here’s why you should add it to your practice.
The first time I met the bar model method I was completely blown away by it. Since then, I’ve seen this reaction again and again with the teachers that I train. It’s a transformational technique for teachers and children alike — particularly children who struggle with maths.
What exactly is a bar model?
Essentially, the bar modelling technique is a form of visual algebra. It’s a method for visualising a maths problem where bars or rectangles represent known numbers and unknown numbers. It acts as a bridge between the word problem and the abstract maths required to solve the problem.
In 2013, the NCETM said:
“We know that when solving word problems, it is often not the calculation that children can’t do — rather they are not sure which calculation they need to do.”
This is especially true with word problems. Pupils can get bogged down in the details of a word problem, most of which has no bearing on the mathematics.
Consider the following word problem:
Sarah, Amir, and Joanna all enjoyed collecting football cards, for their favourite team, Manchester United. They had 60 cards altogether. If they shared them out equally, how many would they each have.
Most of the words in this problem are totally irrelevant, but some pupils need to be taught how to extract the relevant information. One popular way of solving a problem like this is the RUCSAC method: Read, Underline, Calculate, Solve, Answer, Check.
However, this sequence of steps should be used with caution. When you look at this technique more closely, you’ll see that it emphasises process over understanding.
A lot of word problems can contain ambiguous language. Like the following:
How many more than 23 is 27?
This requires the calculation 27 – 23 = 4 which is a subtraction.
But with the RUCSAC method, many children would underline ‘more than’ and think that the calculation required was addition.
What is 4 more than 23?
This requires the calculation 23 + 4 = 27 which is an addition.
The language is very similar, but in this case the calculation required is different.
Enter, the bar model
The best way to help pupils with ambiguous word problems is to develop their understanding. Bar modelling helps children see the deeper structures within a maths problem and lets them construct a model of the problem that easily shows them what calculations are needed.
One of the reasons the bar model has become so popular is it’s simplicity. All you need is a pencil and paper, and it can be applied across the whole range of mathematical topics. In fact, there are only two main types of bar model: the part-part-whole model and the comparison model.
Boost Your Practice with FREE CPD
Receive a CPD boost every time you refer a school! Both you and the referred school will earn a full day of CPD and 2 free places on our 3-day Essentials of Teaching Maths Mastery course (valued at £1700).
Get started on helping struggling schools reach maths success now!

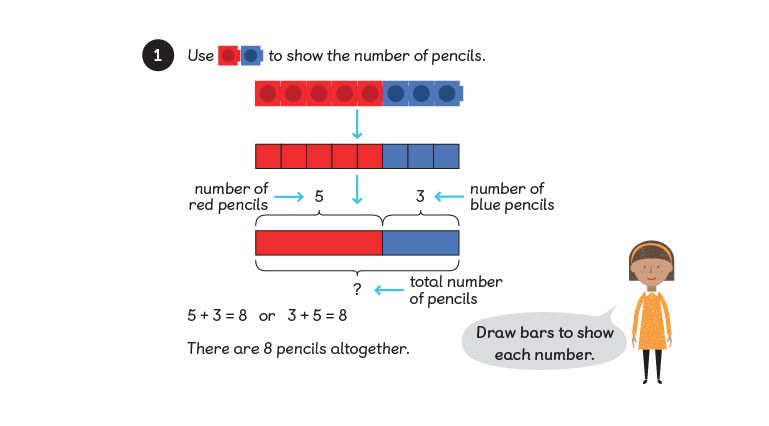
Part-part-whole model
The part-part-whole model can be used for questions involving all four operations, fractions, measure, algebra, time, ratio, proportion and much more.
In the Maths — No Problem! Primary Series the part-part-whole model is introduced like this:
Here we know two parts and need to find the whole. The unknown amount is always represented with a question mark and this tells us what calculation to do. For the part-part-whole model we know two pieces of information and have to find the other. So, we may know the whole and one part and have to find the other part.
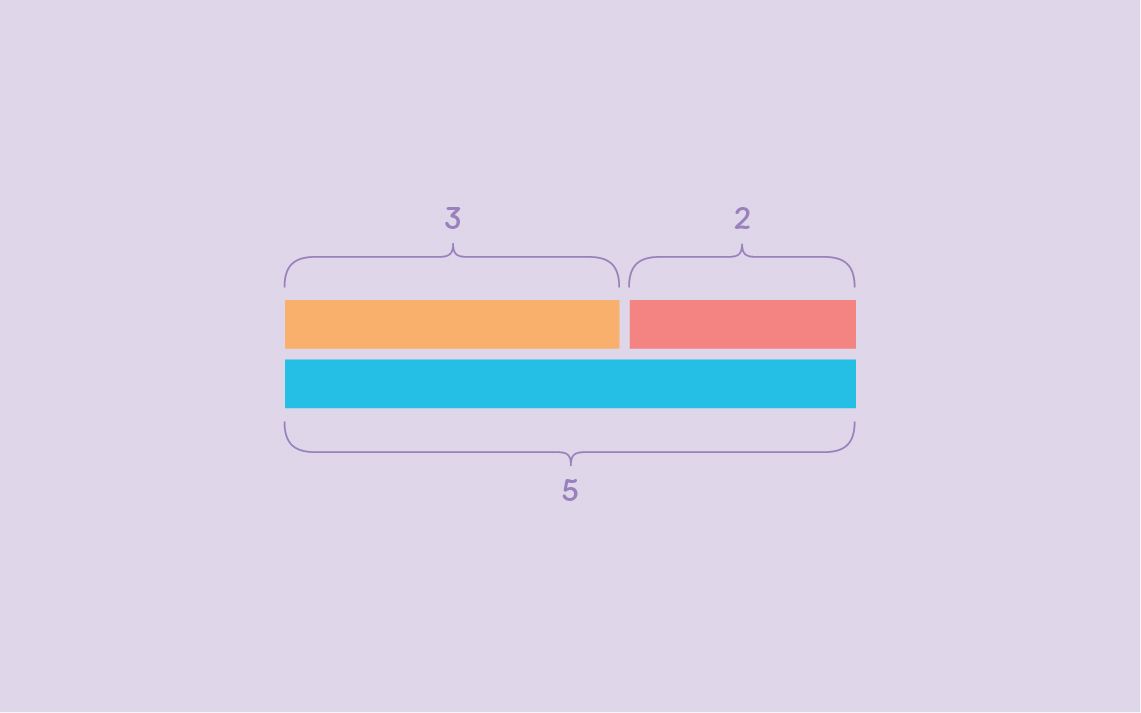
Comparison model
The comparison model is a bit different. Here we’re comparing two bars:
When working with the bar model, we can draw the bars on paper or represent them with cut-out strips of paper, Cuisenaire rods, interlocking cubes or even counters.
In this example we’re looking at a before and after model. This means we need to represent the model at the start of the problem and at the end of the problem after there has been some sort of change.
Sam has 5 times as many marbles as Tom. If Sam gives 26 marbles to Tom, the two friends will have exactly the same amount.
How many marbles do they have altogether?
We can see that we’ve moved two bars so that Sam and Tom end up with equal amounts of marbles. So, two bars must represent 26, and one bar is 13. There are 6 bars in the diagram, so the total number of marbles is 78.
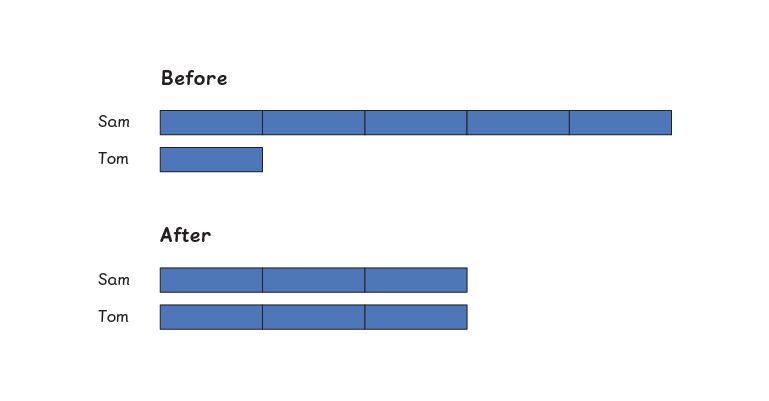
For this type of question, it’s useful to use rods or strips, this way pupils can physically move the bars to show the change.
One of the strengths of the bar model is that it helps children work at a higher level of maths. In the above example, without the bar model we would have to solve the problem algebraically. The solution would look a bit like this:
5x − 26 = x + 26
4x = 52
x = 13
Altogether we have 6x = 78
I’m not sure that many primary-aged children you know who could cope with that, but by using the bar model we have made this problem accessible to children from around age 8 or 9.
Access to higher-level content
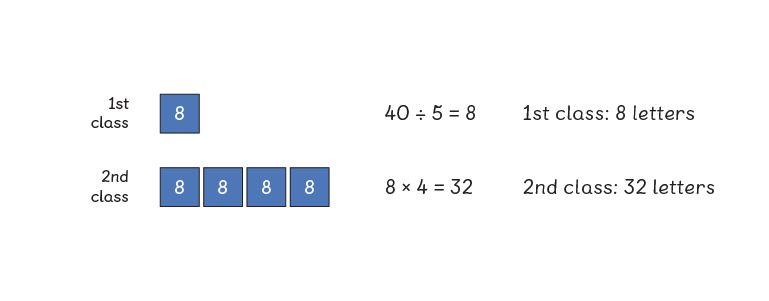
In 2012, there was a question on the GCSE Maths Higher paper, that becomes very straightforward once you know how to use the bar model. I’ve tried this out with primary school children in Year 5 and 6 and they managed it with ease:
Ralph posts 40 letters, some of which are first class, and some of which are second class.
He posts four times as many second-class letters as first. How many of each class of letter does he post?
Try it with your class. It’s possible your pupils will take to it more easily than you do! After all, they haven’t had a lifetime of abstract algebra to contend with.
Check out this video of Maths — No Problem! founder Andy Psarianos explaining the bar model method.