Editor’s note: This is an updated version of a blog post published on March 13, 2013.
How maths mastery prepares pupils
One of the biggest ideas to come from Singapore is the concept of teaching mathematics for mastery. In simple terms it means spending enough time on a topic in order to comprehend it thoroughly.
Teaching for mastery also means that children spend a consolidated amount of time on a topic to understand how it relates to concrete experiences and the real world. This is based on a whole body of research by educational psychologists and specialists, and is reflected in a carefully selected sequence of lessons that children go through. It took the Singapore education system decades to perfect the idea of maths mastery and it is still undergoing improvements.
When talking to teachers and department heads, I often hear that Year-5 and Year-6 pupils aren’t really equipped to problem solve. This is a widespread phenomenon that doesn’t only exist in the UK. The 1983 Cockcroft report said we need to put problem solving at the heart of mathematics education, but how do we do that?
The maths mastery approach gives pupils the fluency they need in the three key components of problem solving:
- Number sense
- Recognising patterns and connections
- Visualisation
On one of my recent school visits, we took an example from a Year-6 workbook and went over how children can solve this problem.
Question from a Year 6 workbook
Mrs. Singh bought a set of furniture for £1760. This was 20% less than the usual price. Later, Mrs. Singh sold the same set of furniture for 5% more than the usual price. How much did Mrs. Singh sell the set of furniture for?
We know that visualisation is key and it is something pupils will have learned early on, therefore we are going to draw this out in a bar model that looks something like this.
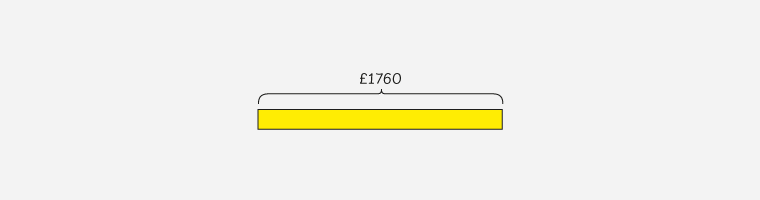
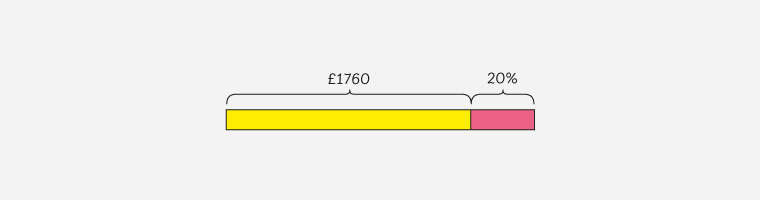
The next thing to represent in this model is this idea that £1760 represents the purchase price once 20% has been taken off the normal price.
Two key things need to happen here:
- Pupils need to be able to accurately depict the 20% off in the diagram
- Pupils need to be able to represent percentages as fractions in order to depict the information correctly on the diagram
Now, this is where a strong number sense becomes crucial. A pupil should be able to recognise that 20% is the same as one-fifth. By recognising this fact they will realise that £1760 is four-fifths of the final price.
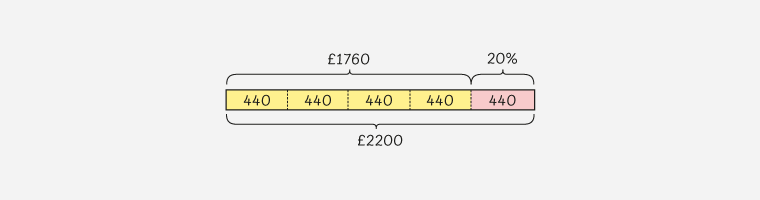
So now we have an opportunity to work out some numbers using mental strategies that have been reinforced in previous years. Here are two possible approaches:
1. Divide by two and divide by two again
2. Simplify the numbers to make it easy to divide
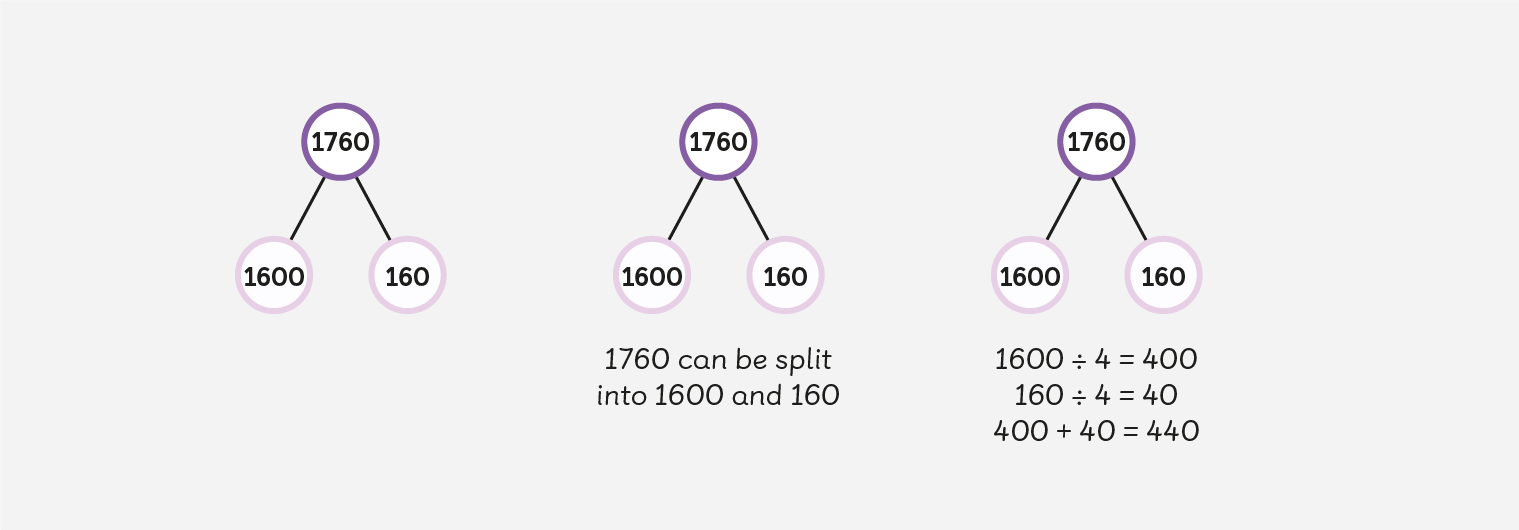
So now we add these facts to the model and work out the ‘normal price’.
By persistently reinforcing the value of mastered skills, these ideas stick. Being able to understand that 20% is the same as one-fifth, for example, is valuable information to solve this problem, but pupils will only remember and use this meaningfully if it was taught with comprehension in mind — not as a series of procedural steps to memorise.
This is why teaching for mastery allows students to solve problems. Teaching isolated procedures is easier, but it doesn’t give pupils the relational understanding they require to make decisions when solving problems. The ultimate goal of teaching mathematics is not to create students who can memorise procedures in isolation, but to create thinkers. Only then can they progress to solve problems.
