Developing children’s mathematical understanding with a variety of representations

In mathematical terms, we use the word representations as one way of labelling the many methods and strategies we may encounter. This definition of representations may be useful in understanding this further:

We also need to challenge the notion that there’s only one right way to approach a problem. It’s a reminder that mathematics is wholly creative and we should embrace the differences in the representations we see.

Can you imagine if there was only one representation of a cake, chocolate or ice-cream?

Understanding representations within the CPA approach

You may be familiar with the Concrete, Pictorial, Abstract (CPA) approach developed by Jerome Bruner.

Put simply, a mathematical problem can be represented using concrete or physical materials, the problem can then be represented using a diagram or picture and the same problem can be represented in the abstract, using symbolic notation:

• 1, 2, 3
• + , -, =.

Within these approaches there are variations and different representations, but they continue to represent the same problem.

How to make sure children have access to multiple representations

It’s important that children have access to different representations of the same mathematical idea or concept. Once they’ve grasped how different representations work, they’ll be on the road to understanding how and when to use them.

1. Teach representations in the correct order

To ensure different representations don’t lead to confusion, the order in which they are presented has to be well thought out. Then, any variation in the representations acts as a support and challenge in a learner’s development of new mathematical ideas.

The following example from Maths — No Problem! Textbook 5A shows a carefully planned progression through a range of representations. The lesson, as with all of the lessons in the series, starts with a single problem:

How many seats are there in this theatre?

There are 28 rows of chairs and there are 26 chairs in each row. This pictorial representation of the problem suggests three separate arrays (28 x 8, 28 x 10 and 28 x 8) which should prompt learners to realise that this is a multiplication problem. They may also realise that the three arrays can be brought together to represent the equation 28 x 26 = [ ]

At this point, children can explore the range of mathematical strategies they know to solve the problem. When these are written down or shown, they become representations of the problem. These representations help develop the ideas and concepts that can be used to solve the problem.

The learners are then given an opportunity to read the textbook and in doing so, have access to a range of carefully structured representations demonstrating the initial problem.

2. Link initial concept exploration with the representations in the textbooks

The link between the first stage of the lesson (discussing and exploring an initial problem), with the representations in the book is crucial to children’s learning. This encourages learners to compare their strategies and approaches to those shown in the book — giving them an opportunity to make connections and relate mathematical ideas.

Here’s an example:

There are 28 rows. Each row consists of 26 seats. There are 728 seats.

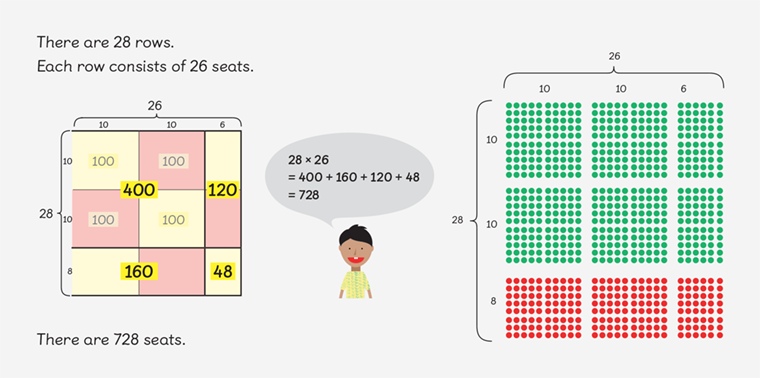
The first representation is pictorial. It shows the array of seats in the theatre and connects this to a multiplication strategy using number bonds to break 28 into 10, 10 and 8, and 26 into 10, 10 and 6.

Maths — No Problem! character Ravi gives support by reminding learners that the groups of seats will need to be added together to find the total number. This pictorial representation is particularly useful as it provides links to earlier ideas relating to ten that could be used to support struggling learners.

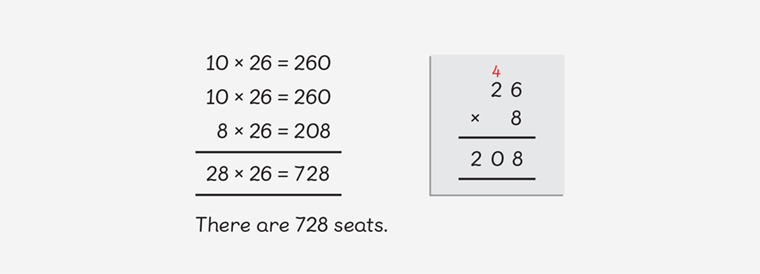
3. Ask learners to use their prior knowledge to solve more abstract problems

The next representation you see doesn’t have pictorial support. But because the previous example did, the link between the pictorial representation and the abstract representation has been provided. To further develop this link you can ask your learners:

“Where do we look when we read 10 x 26 = 260?”
“Why are there two equations that are the same?”
“How do the equations relate to the seating plan?”

These questions relate the mathematics to the problem, and children can start to see the relationship between the different representations.

4. Support learners’ understanding of mathematical concepts

The use of language, written words and reading maths is essential to a learner’s understanding. This idea is continually being developed and built upon. Revisiting these ideas again and again within a spiral curriculum is a key component of a maths mastery approach.

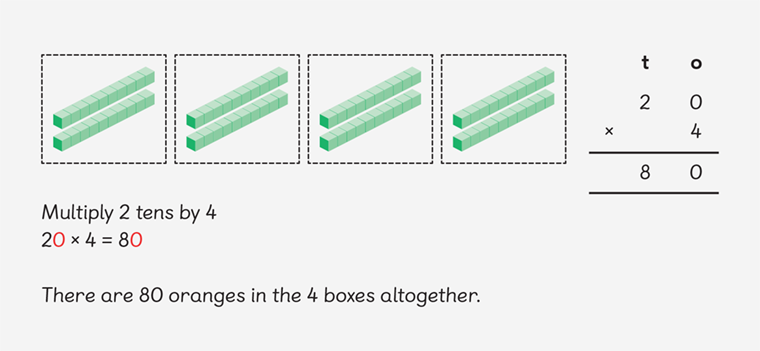
A lesson from Maths — No Problem! Textbook 3A, two years earlier, provided the basis for Sam to be able to relate 26 x 2 to 26 x 20.

As teachers, we can also use this earlier lesson to support children’s understanding if they are struggling to make that connection for themselves.

26 x 20 = 26 x 2 tens
26 x 2 tens = 52 tens
52 tens = 520

Sam also understands that if he doubles the number of groups, or the number of items in the group, he can systematically work through the problem. Again, you can relate this to the pictorial representation in the second example.

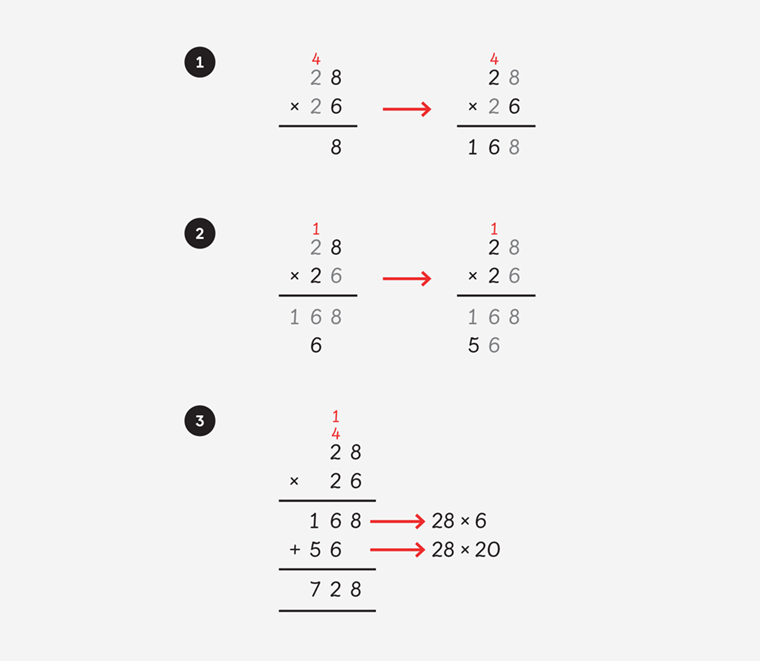
The final example in the book is another abstract method — often referred to as a formal written method. The orientation and directionality of the calculation has changed, however, at each step of the problem, the numbers relate to the previous examples and the original problem.

The goal of maths mastery is for learners to get to a point where they no longer have to attend to certain functions as they solve a problem. In this example, we would want the children to just know that 28 can be broken into smaller parts or just know that 6 x 8 is 48. That way, they can concentrate on new ideas that are associated (in this case, with multiplying a 2-digit number by another 2-digit number).

In the examples above, a carefully structured approach provides representations that allow children to develop their understanding of multiplication.

Teaching multiple representations is a core part of learning mathematics. It’s exciting to make new connections in the representations we have access to.

In a time where blended learning is becoming increasingly widespread, so too is the opportunity to see and interpret different representations. Whether it be representations family members, friends, online resources or books, these different representations should excite, not dull our sense of curiosity. We should use it as a challenge to see the mathematics that connects the various representations.