How to put Bruner’s key theories into teaching practice
Editor’s Note:
This is an updated version of a blog post published on 30 Apr 2018
“Please don’t help me,” I said to my husband as I took the wrapping off a set of flat-pack cardboard shelves that needed folding and shaping to be ready for use…
Construction is not my strong point but, embracing a growth mindset, I wanted to see if I could work it out myself, and overcome the moments when I got stuck. I looked carefully at the pictorial instructions and began. I looked at them again, realised my mistakes and followed them more carefully. I tried things out even when I wasn’t sure and finally after a number of corrections, I had completed the challenge. I sat back and realised that I could in fact do it. I recognised the logic of the steps, and could see how the tearing, folding and shaping had to be done in sequence.
“The most effective way to develop a coding system is to discover it rather than be told by a teacher.”
– Jerome Bruner
Share your success, be rewarded
Everyone needs a break. Especially the kids that are missing out.

My “teacher” (in this case, my husband) had not told me what to do. Instead, I made a series of discoveries on my own. I’m much more likely to remember them next time — when we make our own discoveries, they become more meaningful and deeply embedded.
In the 1960s, American cognitive psychologist Jerome Bruner called this the constructivist approach — the way in which we construct meaning for ourselves. This approach is around us every day in the classroom; pupils are constantly constructing and reconstructing their understanding of the world as new experiences and interactions occur. One of the challenges we have as teachers is to facilitate this rather than doing it for them.
Bruner advocates that “a good teacher will design lessons that help students discover the relationship between bits of information. To do this a teacher must give students the information they need, but without organizing it for them” (Saul McLeod). In effect, we provide the tools, the initial task, the questions and the opportunity for exploration and discovery rather than methods and procedures.
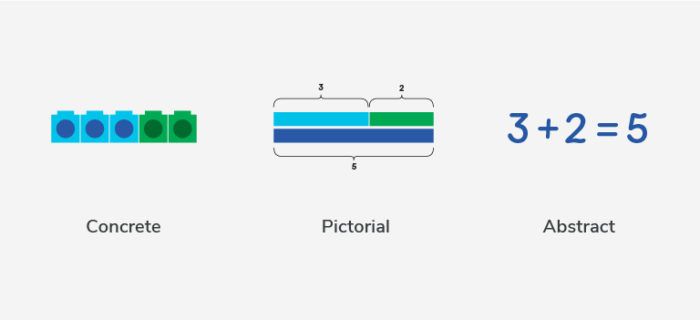
The CPA Approach
Springing out of Bruner’s emphasis on the heuristic nature of learning (that is, trial and error and self-discovery) are his three Modes of Representation. Bruner identified that learning occurs through enactive means (doing, which is action based), iconic means (seeing, which is visual) and symbolic means (abstract, which is in the form of ‘codes’ or symbols i.e. language).
This Concrete, Pictorial, Abstract (CPA) approach lies at the heart of Maths — No Problem! It enables a natural and supportive progression for learners as they develop their understanding and skills in maths. For example, last week I explored equivalent fractions with my pupils. We began with multi-link cubes, progressed to the pictorial problems in the book and then on to questions with no visuals provided except numbers and the necessary mathematical symbols. This resulted in a fully embedded understanding of the concepts throughout the classroom.
The Importance of Bruner’s Scaffolding
Guiding students through the lesson and providing opportunities for pupils to make the next steps in their learning is also fundamental to the structure of Maths — No Problem! Last year, I witnessed this in action when my teenage daughter took on the somewhat ambitious task of making her own gingerbread house from scratch during the holiday season. She gathered her ingredients, carefully selected the sweets she would decorate it with, and got to work. Once the dough was made, she began to roll it out using a template to mark, and cut out the rectangles for the sides. Again and again she rolled out the first piece of dough and could not get the template to fit with the dough at the required thickness. I came alongside and asked her if it would make any difference if she rolled the dough from a rectangle shape rather than an oval. She tried it and it worked. What was an obvious solution to me was not yet known to her. What she needed was someone suggesting a step forward.
This in effect is what Bruner, building on Lev Vygotsky’s work, coined as scaffolding. We can define this as “the support an experienced adult — a parent or teacher, for example — provides to assist the natural development of a younger, less experienced learner in their voyage of discovery” (Alex Moore).
How Spiralling Improves Learning
It is vitally important that we also acknowledge the provisionality of learning; that we might return to a subject and make fresh discoveries, allowing us to change our minds about our previously perceived notions.
Recently, whilst watching David Attenborough’s “Blue Planet II” series, I sat in awe at seeing the previously undiscovered creatures living at the bottom of our oceans. “Who would have thought it?” I found myself saying as I realised my understanding of the world had changed. Throughout our lives, we all experience this process of learning, revising, and revisiting as we return to old concepts and make sense of new one’s.
Bruner termed this spiralling; the process of coming back to an area of learning to build upon it in light of new discoveries. This is the framework the Maths — No Problem! approach provides. Pupils can build on their learning as they progress through the programme — revisiting familiar concepts and building further on them. Spiralling may also mean we take steps backwards before progressing forward — something to consider when a pupil is not moving forward as we might anticipate.
Last week, as I reflected on a maths lesson that hadn’t gone so well, I saw what I could have done to make it work better. This was not about the class having to do something differently: it was how I could have taken a different approach. Bruner himself was an advocate of reflective practice. This means turning the situation back on ourselves, looking at our own practice and learning, in order to understand how our pupils might be experiencing and managing their learning. This is a practice that helps us step away, take a breath, and find perspective. Because when it comes to our profession — we’re learners, too.
Go beyond Jerome Bruner
Interested in learning more? Help your learners develop problem-solving skills with a teaching approach that bridges the gap between influential theory and in-school practice.
