Walking in a winter numberland: activities for KS1

Okay, so you probably don’t have a fireplace and mince pies in your classroom. But you can still add a little magic to your lessons. Created for children aged five to eight, why not try these maths problems in your classroom tomorrow?

Year 1: add by counting on

If you follow the Maths — No Problem! scheme of work, you can use these questions alongside Textbook 1A, Chapter 7, Lessons 1-2.

For this maths problem, you’ll need:

• Counters
• Ten frames

Lesson objective: add by counting on from the largest number.

There are 7 penguins on an iceberg. 4 more penguins arrive. How many penguins are there now?

Get started by giving your learners ten frames that are already filled with 7 counters. Tell them there are 7 and have them verify this. Ask them to place 7 counters on a copy of the ten frames to represent the penguins.

Then tell them you are going to add 4 more penguins. Ask them how many they have now. How many ways can they figure this out?

For struggling learners, you can use counters to represent this problem. Use a tray or a container with 7 counters and have 4 counters in your hands. Tell the pupils that there are 7 counters in the tray and you want to add 4 more. How could we do this? Both the count all method and count on method should be discussed.

There are 5 snowmen in a field. 8 more snowmen are built. How many snowmen are there now?

Ask them if it’s better to count on from the largest number or from the smallest? Is starting from 1 easiest? If we already know how many are in the large group, do we need to count them all?

Consistently asking the question of whether we need to count all of the items when we already know a group has a specific amount will help learners figure out that there’s no need to count all of the items in the large group.

Ask your advanced learners what they should do if the bigger number is not first in the question. Does it make a difference if it’s first or second when we’re adding? Why or why not? Ask them to explain their reasoning.

Year 2: compare the mass of three objects

If you follow the Maths – No Problem! scheme of work, you can use these questions alongside Textbook 2A, Chapter 6, Lesson 5.

Lesson objective: To compare the mass of three objects and use appropriate vocabulary.

Begin this lesson by showing the class 3 jars that all weigh the same when empty. Fill them up with different items and ask learners if they can tell you how they could compare the different masses. Use their suggestions to talk about the same amount of objects that could have different masses.

Then show pupils this task and give them time to discuss what they should do to solve this problem.

3 jars all weigh the same when empty. The jars are filled with different items. How do we compare the masses of the jars?

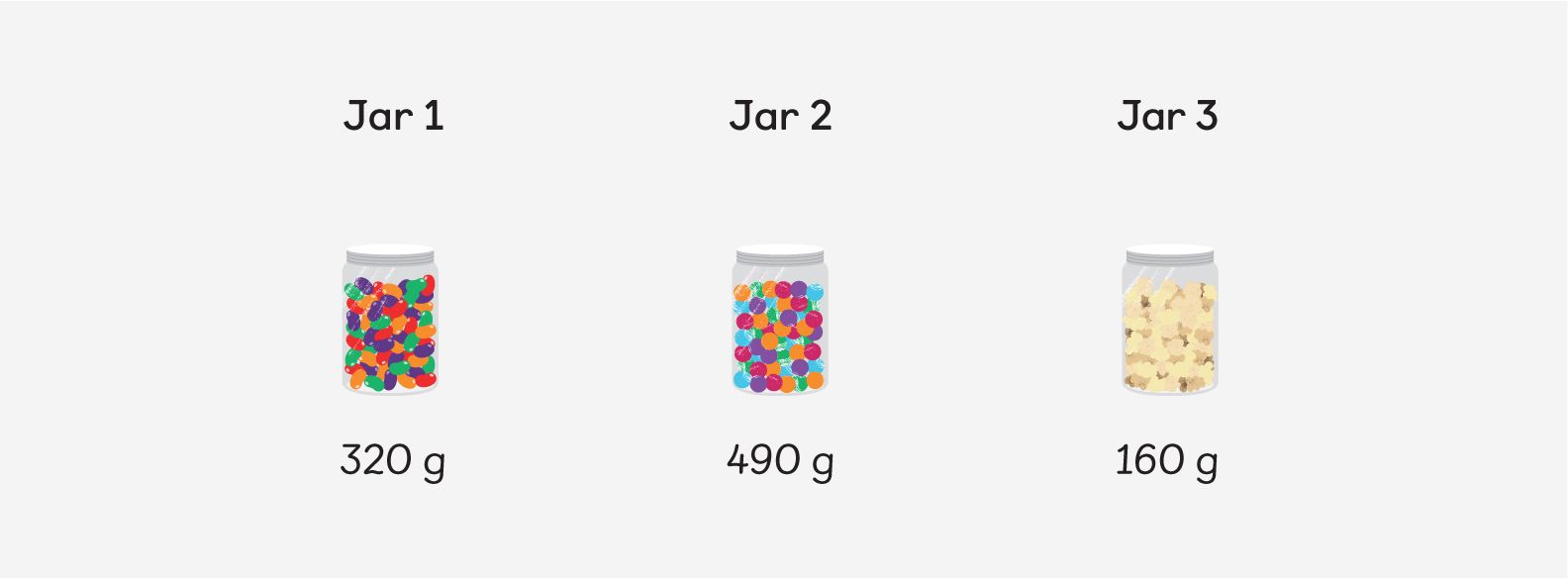
Encourage use of the language ‘lighter/lightest’ and ‘heavier/heaviest’. Ask learners how they would solve the problem to find the difference between two of the jars.

Model the subtraction calculation and ask them to order the jars from lightest to heaviest. Have different containers that learners can weigh in groups and ask them to come up with a conclusion to practice their vocabulary.

Now ask your learners another question.

Compare the masses of 3 reindeer:

• Comet: 85kg
• Dasher: 115kg
• Rudolf: 92kg

1. Who is the heaviest?
2. Who is the lightest?
3. Rudolf is ______ kg heavier than Comet.
4. Arrange the reindeer from lightest to heaviest.

Encourage learners to sort the reindeer in the correct order from lightest to heaviest. Ask them to draw comparisons between the reindeer in the problem.

To assess your learners ask them:

Can you correctly measure the mass of items in kilograms?
Can you use a table to record their findings systematically?
Can you use the terms ‘greater than’, ‘less than’, and ‘heavier than’, ‘lighter than’?
Can you use the correct symbols for the terminology?
Can you compare the mass of more than two items?

Year 3: solve word problems

If you follow the Maths — No Problem! scheme of work, you can use these questions alongside Textbook 3A, Chapter 4, Lesson 9.

Lesson objective: To solve word problems that involve multiplication.

To start the lesson, show you learners this question:

There are 18 blue scarves in a shop. There are twice as many green scarves as blue scarves.

1. How many green scarves are there?
2. How many scarves are there altogether?

Discuss the problem with your class. What key information is given? 18 blue scarves; twice as many green scarves. What is the problem asking us to find? The number of green scarves; the total number of scarves. Give them some time to work on this.

Using bar models

How could we represent this maths problem using bar models?

Begin moving pupils in this direction through questioning, giving them time to work it out for themselves. Only use questioning when pupils are unable to move forward on their own. How can we draw the bars to represent the scarves? Which one should be larger?

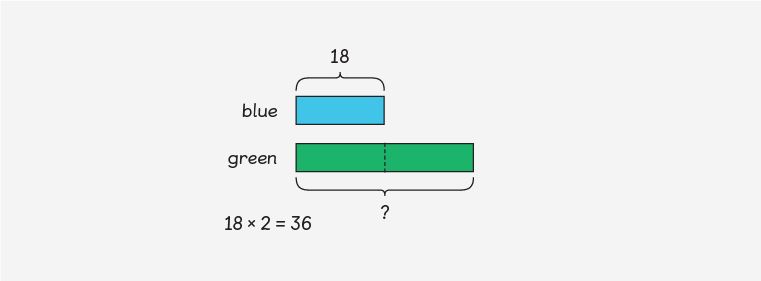
Use coloured paper or card to represent the bar for the blue scarves. How large should we make the bar for the green scarves? Having the same sized bar for both colours means we have the same amount, so we need the green bar to be bigger.

The problem says there are twice as many green scarves as blue scarves, so we need to have two bars which are each the same size as one blue bar.

What value does the blue bar represent? So how can we work out the value of the green bar?

It is twice as big as the blue bar: 18 × 2. How can we multiply 18 by 2? (10 × 2) + (8 × 2). Therefore, the number of green scarves is 20 + 16 = 36.

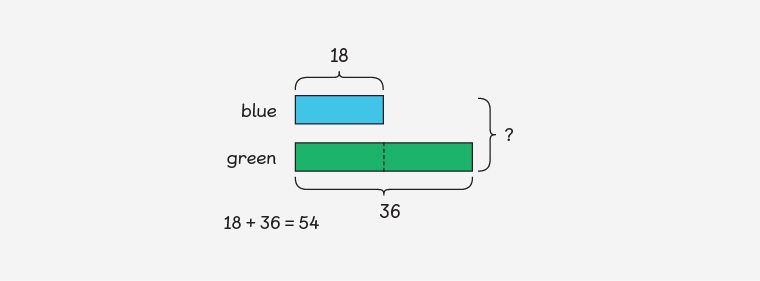
What calculation do we need to do to work out how many scarves there are altogether? There are 18 blue scarves and 36 green scarves. So we can add the amount of scarves together to find the total. 18 + 36 will give us the total number of scarves.

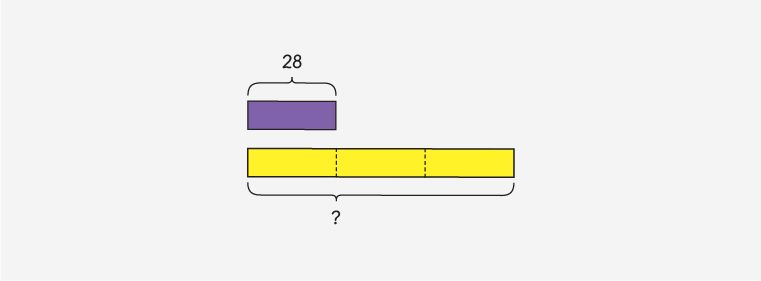
Now try this.

There are 28 mince pies on a tray.
There are 3 times as many gingerbread biscuits as there are mince pies.

1. How many gingerbread biscuits are there?
2. How many treats are there in total?

To assess your learners ask:

Can you use the bar model heuristic to represent number problems?
Can you represent numbers proportionally using the bar model heuristic?
Can you multiply or divide when appropriate?

An extra challenge

If you’re an avid Maths — No Problem! blog reader, you’ll know how much we love journaling. So why not challenge your learners to invent their own winter-themed questions and record them in their journals. The more creative, the better!

We’d love to see what your learners come up with. Share your journal entries with us on Twitter by tagging @MathsNoProblem

We hope you’ve had an inspiring and productive year. Now put down your textbooks and have a relaxing winter break. You deserve it.

This blog was originally published on Dec. 16, 2019 and updated on Dec. 16, 2021.