This questioning technique strengthens maths lessons and challenges advanced learners
Looking for ways to strengthen your maths lessons and challenge your advanced and adventurous learners? It’s easier than you think.
A big challenge of whole-class teaching is providing stretch and challenge for all of your learners. Giving children different supplementary material can be a minefield and a logistical challenge.
There are three broad options I use to support my learners: journalling, the Mathsteasers Series and ‘strengthening’ the way I use the Maths — No Problem! textbooks and workbooks.
So, what do I mean by strengthening a lesson?
Strengthening a lesson means adding the right amount of depth and complexity so all learners feel challenged. This is especially helpful when it comes to stretching your advanced learners, but all learners benefit from strong maths lessons.
Here’s how one question can add depth and complexity to your lessons.
How do you strengthen a lesson with a questioning technique?
As you repeat teaching a year, you’ll start to develop a repertoire of add-on material and mathematical variations. This is what adds complexity and depth to your lesson. You can use add-on material with a small group, or with the whole class — but remember to include the fundamentals of discussion and sharing approaches.
One of my favourite strengthening questions is: “What other questions could you ask?”
So simple, yet so effective. And the best part? You can use this line of questioning with any topic throughout Key Stage 2.
Let’s take a look at how you can use this question to strengthen a lesson.
Strengthening a Year 6 decimals lesson
This example is from Maths — No Problem! Textbook 6A, Chapter 4, Lesson 9, and covers multiplying decimals. The objective of this lesson is ‘learners can multiply one-digit numbers with up to two decimal places by one-digit whole numbers, with regrouping’.
To begin the lesson, I started my class off with the In Focus task (or anchor task).

Most of my learners tackled the problem systematically, for example, starting with ×9, then ×3 and finally ×2.
You can see the final 18 results below. It’s also worth having a quick discussion about whether there are actually 19 answers if you include all the combinations that multiply to zero.

Instead of moving straight to Guided Practice, I gathered the class together and asked: “Take a look at the set of data, what other questions could you ask?”
My class came up with a list which ranged from the obvious to the more challenging. After writing the questions on the board, we discussed which questions might be harder so learners could decide, in their pairs or threes, the level of challenge they wanted. My learners then completed the answer in their journals.
Here are the journal entries from the lesson:
Question #1: What is the total?
This seemingly straightforward question lets learners review adding decimals. The first example shows a confident learner who added up the three groups with clear working. They then combined the three totals to work out the final, overall total.

The next example shows a learner working carefully, but it’s clear they’re not as confident in their adding. They’ve added one decimal at a time to gather a running total. When two of their totals didn’t match other groups, they checked back through to find that they had made a mistake on the first sum.

Question #2: What is the highest and lowest product? What is the range?
Finding the range is a straightforward calculation that can be done mentally or by using a written method. Here the learner found the biggest and smallest number and found the difference using a written method.

Question #3: Write the decimals in ascending and descending order
Reading decimals and their place value should be within reach of most learners. By writing an ascending or descending list, children soon spotted they could copy it out in reverse! The class discussed whether writing the decimals in ascending order might be slightly easier because we generally learn to count up with numbers.

Question #4: Investigate how rounding affects the total
This question is an excellent example of an advanced learner going one step further. Having found the totals of the decimals, they rounded each decimal to the nearest whole number and added them up.
The learner then asked, “did the sum of the whole numbers match the total if you added all the decimals and then rounded the answer?” Then they reasoned why the answers were (slightly) different.

The reason that this answer is different from what the other answer would be rounded is because more numbers were rounded up here than in the other answers.
Question #5: Find the mean
Finding the mean meant remembering how to do this from Year 5 work. With a ‘no calculator’ rule, this involved quite a hard division sum. Learners worked it out and explained how in the example below.

I found this by adding all of the products up and then dividing it by the amount of products there is, in this case the sum is 226.44 ÷ 18 = 12.58
Question #6: What if the question involved tenths instead of hundredths?
What would happen if you moved the decimal point, so you are looking for tenths rather than hundredths? There are still 18 combinations, but there’s a greater range to investigate once you’ve got all the totals.
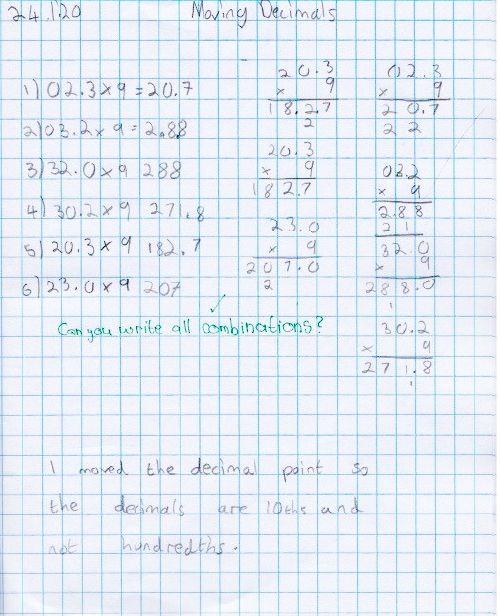
Question #7: What if you were adding instead of multiplying?
The learners chose whether to add the number to the whole or the hundredth. They soon found that the difficulty level was low as there’s no renaming.


Question #8: Can you convert the products to fractions?
This question gave learners that chance to revisit concepts from the previous fractions chapter, including simplifying to the lowest form.

Question #9: Find the median
This is one of the more challenging problems as there are two middle numbers with a gap between 0.90. This learner worked through the problem and wrote an explanation for others to follow.

The middle number is 8.25, because the number of numbers is 18, and 18 doesn’t have a middle number. You have to find the 8th and 9th [correction to 9th and 10th], find the difference, half it and add it on to the 8th [correction to 9th] number.
Did my learners find the lesson challenging?
Even though there was considerable productive struggle, my learners stayed focused throughout the lesson. I think they managed to successfully operate the lesson because they were already familiar with the dynamics of a regular MNP lesson.
Time constraints meant that one group didn’t get around to answering all of their questions. However between them, the class found all the solutions. Asking all of the groups to contribute to a discussion served as a strong plenary at the end.
This type of lesson is quite open — your learners get to choose what they want to do and will (hopefully!) enjoy their independence. They also have the chance to revisit and consolidate prior learning in a new context.
Sometimes new channels of investigation will open up, which gives learners the chance to divert and explore. By expanding and exploring the original anchor task, learners avoid accelerating to new learning and concentrate on number work, problem-solving and working together.
