Maths Mastery Guide

Introduction

Whether you’re a teacher attempting to navigate the complex world of mathematics education, a parent trying to make sure your child gets the best possible maths instruction, or a school leader needing to decide how best to invest limited resources, you’ve likely heard of maths mastery.

There are many misconceptions surrounding maths mastery, but have no fear! On this page, we’ll:

• Take a deep dive into the fundamentals of maths mastery
• Explore the history of maths mastery and Singapore maths
• Look at how the Singapore method arrived in the UK
• Examine some specific theories like Bloom’s Taxonomy and the CPA approach
• Talk about the individual and societal impact of poor numeracy
• Give you some practical teaching tips from experts in the field

What is Maths Mastery?

Maths mastery is an approach to teaching that gives pupils a deep, long-term, secure and adaptable understanding of mathematics.

The concept of mastery has its roots in the mastery model developed in the late 1960s by Benjamin Bloom, an American educational psychologist.

The mastery approach currently being promoted in the UK shares some features with Bloom’s mastery model, such as the focus on a uniform degree of learning for all pupils and the desire for students to achieve a deep understanding of mathematical concepts.

However, a stronger focus on structure, early intervention and the consistent use of representations differentiates the UK approach from other models.

The core elements of the UK approach to mastery, as succinctly outlined by the National Centre for Excellence in the Teaching of Mathematics, are coherence, representation & structure, mathematical thinking, fluency and variation. More on that later.

How is mastery different from conventional approaches?

Teaching for mastery differs in many key respects from more traditional methods, perhaps most fundamentally in the idea that everyone can learn.

In a conventional primary maths lesson, children are placed in different groups and given different content based on their perceived ability. From an early age, therefore, children are labeled as those who can do maths and those who can’t.

This can be devastating.

It can also be avoided.

The mastery approach rejects the idea that only some children can do well in maths. It embraces the idea that everyone can do well, regardless of prior attainment.
Teaching maths for mastery offers all pupils access to the full maths curriculum. This inclusive approach and its emphasis on promoting multiple methods of solving a single problem builds self-confidence and resilience in pupils.

As George Pólya said,

“It is better to solve one problem five different ways, than to solve five problems one way.”

With a mastery approach, the whole class moves through topics at broadly the same pace. Each topic is studied in depth and the teacher doesn’t move to the next stage until all children demonstrate a secure understanding of mathematical concepts.

This approach encourages learners to share ideas and try out different methods of problem-solving, says Roger Hitchin, head of Singapore maths and drama at Wellington Prep School. You don’t see the forest of hands from learners who are ‘stuck’ because with mastery, learners are less reliant on the teacher — they work with different children, model answers in front of the class and ask each other when they’re not sure.

Although they don’t realise it, learners quickly gain confidence during this type of lesson. They use mathematical vocabulary freely, don’t mind making mistakes and get used to explaining what they’re doing.

Traditionally, the goal for teachers has been to accelerate pupils into the next level as quickly as possible. The result was rapid advancement with superficial learning and insufficient depth.

Teachers have become accustomed to the idea that they will have at least three different groups in their classroom. There will be a handful of advanced learners, a handful of learners who are behind, and the rest somewhere in the middle.

One key aspect of the mastery approach, in contrast, is the embedded expectation that all children will achieve.

How do you teach a whole class while still meeting the needs of all pupils?

The mastery approach aims for depth. Teachers don’t accelerate a small group of pupils. Some pupils, however, are thinking more deeply than others.

This type of differentiation doesn’t mean leaving out harder topics for struggling learners, or adding in trickier concepts for more advanced learners. The same topic is taught ⁠— so all children achieve the same learning ⁠— but the depth of learning is varied.

Differentiating through depth of learning gives teachers a huge classroom advantage, says Oxford University Press Editor Laura Connell. Differentiation strategies help meet children’s individual needs while keeping the whole class learning at the same pace.

This way of teaching gives learners the opportunity to understand concepts at a relational level, rather than as a set of rules or procedures.

The slower pace leads to more efficient progress because it ensures students are secure in their understanding and teachers won’t need to revisit topics.

A teacher in a 2015 trial project on mastery teaching had this to say about the results:

“The big success in year 1 is the achievement of those children who have struggled with maths. If maths had been taught in the way we have done previously, then that cohort would have been progressing to year 2 with a wide range of attainment. As it is, the gap is much narrower.”

In interviews with the pupils, it was apparent

“they were more fluent, faster and their recall was much improved.”

The mastery approach contains built-in challenges to keep advanced learners engaged. For instance, the placement of an answer may vary. Rather than coming at the end of a question, it may be at the beginning or in the middle.

Sometimes an answer is a number, other times the learner has to specify whether the amount increased or decreased.

Low Threshold, High Ceiling

While the first question may be straightforward, subsequent questions deliberately involve numbers and operations that take learners over 10, 100 or 1,000. The difficulty builds gradually, providing scope, challenge and rigour for all attainment levels.

These exercises are called low threshold–high ceiling. With an LTHC approach — one grounded in the growth mindset philosophy of Carol Dweck and popularized by mathematician Jo Boaler — advanced learners will always be engaged and challenged.

This highlights how learning under the mastery approach gradually ramps up in difficulty. Learners draw on multiple methods and their peers to solve problems.

Mastery mindset

According to Debbie Morgan, NCETM Director for Primary, mastery of mathematics is achievable for all and leads to deep and sustainable learning. It also develops:

• The ability to build on something that has already been mastered
• The ability to reason about a concept and make connections
• Conceptual and procedural fluency

What does it mean to master something? Think of learning to ride a bike. Once you know how, it becomes automatic. You’re good at it. You don’t need to think about it. You can show someone else how to do it.

Teaching for mastery requires the belief that all pupils can achieve. It means teachers must keep the class working together so all pupils can access the curriculum. It means spending more time on key topics, so students can go deeper and embed learning.

“If a pupil fails to grasp a concept or procedure, this is identified quickly and early intervention ensures the pupil is ready to move forward with the whole class in the next lesson,”

the NCETM says in its helpful primer The Essence of Maths Teaching for Mastery.

The NCETM highlights the Five Big Ideas in Teaching for Mastery. These are:

1. Coherence – Lessons are broken into small, connected steps
2. Representation and Structure – Representations reveal the mathematical structure
3. Mathematical Thinking – Ideas are worked on, reasoned with, and discussed with others
4. Fluency – Facts and procedures are quickly and efficiently recalled
5. Variation – Concept are often represented in more than one way

Teaching maths for mastery is a transformational, evidence-based approach. When taught to master maths, children develop their fluency without resorting to rote learning. They are able to solve non-routine problems without having to memorise procedures.

What does Singapore have to do with any of this?

Maths mastery recently came to prominence in large part because of the success of Singapore maths, a curriculum developed by educators in the 1980s to address what they saw as the country’s chronic underachievement.

The Singapore method emphasises problem solving. Students draw on their ability to visualise, recognise patterns and make decisions to build mathematical fluency.

Singapore maths minimizes the dependency on rote learning, memorisation and other tedious practices that put many people off mathematics forever at a young age.

The goal is to ensure learners grasp core concepts, not just perform empty exercises.
Much of the mastery approach currently in use in UK schools derives from the Singapore method, but the Singaporeans themselves drew on the work of numerous international theorists to create their famous curriculum.

Five Proven Theories

According to legendary educator Dr. Yeap Ban Har, the Singapore method makes use of Five Proven Learning Theories from notable experts Jean Piaget, Zoltan Dienes, Lev Vygotsky, Richard Skemp, and Jerome Bruner.

Jean Piaget

Piaget recommends letting students have ample processing time to accommodate new ideas. This is the reason Singapore textbooks have an anchor task, or a single task that is dealt with for an extended period.

Zoltan Dienes

Dienes advocates learning ideas in an informal way, through exploration, before structured learning takes place. Based on Dienes’ ideas from 1960, systematic variation is used throughout the curriculum.

Variation can take the form of mathematical variability, where learning one particular concept is varied, or perceptual variability, where the concept is the same but pupils are presented with different ways to perceive a problem and to represent a concept.

Lev Vygotsky

Vygotsky emphasises cooperative learning or collaborative structures during learning. His theories of proximal development and scaffolding show how students progress through interactions from the current to the potential area of development.

Richard Skemp

Skemp’s theories on relational understanding and instrumental understanding (http://www.davidtall.com/skemp/pdfs/instrumental-relational.pdf) are key to the Singapore method. The idea is that when pupils understand a concept in relation to other concepts (relational understanding), they can remember and apply what they learned more effectively than when they simply memorise the concept in isolation (instrumental understanding).

Jerome Bruner

Bruner developed the Concrete Pictorial Abstract (CPA) approach, which underpins the entire mastery framework. He also coined the term scaffolding to describe how children build on the information they have already mastered.

In his 1966 research on the development of children, Bruner proposed three modes of representation:

1. Concrete or action-based (enactive representation)
2. Pictorial or image-based (iconic representation)
3. Abstract or language-based (symbolic representation)

Bruner also proposed the spiral curriculum, where subjects are revisited at intervals and at more sophisticated levels. A concept is first represented with concrete materials, then by models, or pictures, and finally by abstract notation, like a plus or equals sign.

Where does Bloom’s Taxonomy fit in?

In addition to these Five Proven Theories, another critical piece of the Singapore method comes from the work of Benjamin Bloom, whose focus on the mastery of learning developed into what’s known as Bloom’s Taxonomy.

The original aim of Bloom’s framework was to give educators a common language to talk about curriculum design and assessment. Today, it’s used by teachers all over the world.

Bloom’s Taxonomy consists of three domains that reflect various types of learning. Each domain has different levels, ordered from the simplest to the most complex and associated with relevant action verbs.

The cognitive domain

• Thinking and experiencing
• The cognitive domain is all about knowledge and mental skills. As you move up the levels, the thinking skills become more sophisticated
• Bloom and David Krathwohl described the original cognitive domain in 1956. Since then, advances in cognitive psychology prompted Lorin Anderson and Krathwohl to publish a new version of the cognitive domain in 2001 with the following features:
  • Remembering: recall facts and basic concepts
  • Understanding: explain ideas and concepts
  • Applying: use information in new situations
  • Analysing: make connections between ideas
  • Evaluating: justify a decision
  • Creating: produce new or original work

The affective domain

• Emotion and feeling
• Learning in the affective domain describes the way people react emotionally and their ability to feel others’ pain or joy. It’s all about the awareness and growth in attitudes, emotion and feelings
• Although the affective domain is part of what we call Bloom’s Taxonomy, it wasn’t described by Bloom. The affective domain was categorised by Krathwohl in 1964 with the following features:
  • Receiving: paying attention in a passive way
  • Responding: active participation
  • Valuing: attaching value to learning
  • Organising: comparing, relating and elaborating
  • Characterising: building abstract knowledge of their own

The psychomotor domain

• Practical and physical
• The psychomotor domain is action-based. It means to change or develop in behaviour or skills. It describes how learning a physical skill begins with observation and progresses to mastery
• Bloom and his research team didn’t complete any work on the psychomotor domain. The taxonomy developed by Elizabeth Simpson in 1972, which describes how physical skills develop, has the following features:
  • Perception: sensing cues for motor activity
  • Set: readiness to act
  • Guided response: imitation and then trial and error practice
  • Mechanism: the growth of a habit and greater confidence
  • Complex overt response: skilful performance and proficiency
  • Adaption: the ability to develop and modify these skills
  • Origination: the ability to create new movement patterns with the new skills

Building on earlier research by Piaget and Vygotsky, Bloom’s work suggests that thinking skills develop through cognitive challenge.

Bloom’s three domains remind us that learning isn’t a detached intellectual process but the sum of what we are understanding, feeling, and actively practicing.

Finally, two papers written in the 1980s were the catalyst for change for Singapore: in the UK, the Cockcroft Report and in the US, An Agenda for Action. Both argued that problem solving had to be the focus in mathematics education.

Why should we care about the Singapore method?

Perhaps nobody outside Singapore would care about the Singapore method if the curriculum hadn’t propelled the country’s maths pupils to the top of the international rankings.

Not only did Singapore manage to change it’s mathematics scores dramatically in a very short time, it has remained in the top three worldwide ever since.

Singapore placed first in the Trends in International Mathematics and Science Studies (TIMSS) and Program for International Student Assessment (PISA) rankings in 1995. It placed 16th less than a decade earlier. It’s an unprecedented achievement.

One of the findings in the TIMSS data is that most countries see a drop in comprehension in year 8. Singapore students, on the other hand, continue to excel, proof of a strong foundational base.

A significantly higher percentage of pupils in Singapore attain intermediate level than in the UK. This suggests challenged learners benefit the most and retain their level.

What makes the Singapore method so effective?

One key pillar of the Singapore method is the availability of excellent textbooks and workbooks.

Wait, what? Textbooks? Workbooks?

We know what you’re thinking. It’s a common reaction.

But for more than 30 years, Singapore has been producing high-quality textbooks that carefully synthesize the ideas of Bruner, Skemp, Piaget, Vygotsky, Dienes and others.

These are not your grandmother’s textbooks

Singapore-style textbooks take students on a journey through carefully crafted lessons, delivering the right learning at the right time. With expert guidance, students make the necessary connections with previously learned material — a la Bruner’s spiral curriculum.

Textbooks are carefully scrutinized by authors, publishers, consultants and the Ministry of Education, a peer review process that acts as a highly effective quality control system.

In the UK, the subject of textbooks is a touchy one. Perhaps no other country has moved further away from textbooks than the UK.

Hayley Kington, a teacher at Saltdean Primary School, sums up the mainstream view.

“When I heard textbooks and workbooks, I thought, it’s going to be very dry, they’ll be old, it’ll just be pages and pages of sums and calculations.”

That was until she started using a Singapore-style textbook, in this case, the Maths — No Problem! Primary Series. She went on to say…

“When you look at them, they’re really visual, they’re colorful, they show pictorial representations, they show a visual, so they really hook the children into what they’re doing, and help them to understand the concept of what they’re doing,”

And the benefit?

“It allows teachers time away from making those worksheets and trying to find those worksheets online. It gives them time to do the assessment, to do the feedback, the marking, all those things that are so much more important than spending an hour making a worksheet.”

The Maths Hubs Programme’s evaluation of the textbook project conducted between January and June of 2015 found more than 90% of schools reported overall success when using Singapore-style textbooks to support the development of primary mathematics teaching for mastery.

It also found increased teacher subject knowledge and confidence and a positive impact on pupils’ attitudes to learning and attainment.

Louise Hoskyns-Staples, senior lecturer in mathematics education at the University of Worcester and a national maths lead, said she’d seen many textbooks over the years, and “most were dull at best and at worst caused pupils problems in understanding concepts, often repetitive, and designed to embed a single method but requiring very little deeper thought or problem solving.”

But that was before she came across the Singapore-style textbook, which she later implemented throughout the school.

“The clear child-friendly word and pictorial problems at the start of each lesson ensure that problem solving is a method of teaching rather than something tacked on at the end,” she said. “By exploring these problems, pupils get used to unpicking the maths that is contained within.”

Today, thousands of schools across the UK, as well as the Department for Education’s Maths Hubs have adopted Singapore-style maths textbooks.

But it’s not just the introduction of high-quality textbooks that made the Singapore method so successful. The other key pillar was the creation of a coherent teaching model that included professional development and generous support for teachers, which allowed them to continuously reflect and improve their methods.

Teacher training is at the heart of the success of Singapore maths, with good-quality professional development always high on the agenda. Aspirations, goals and expectations of the learning are clearly laid out and continuously discussed.

How did Singapore Maths get to the UK?

Maths — No Problem! is widely credited with bringing Singapore maths to the UK.

Dr. Anne Hermanson and Andy Psarianos created Maths — No Problem! after their daughter fell behind in maths when transferring schools. After researching the subject and after Andy’s time spent in Singapore they found the Singapore method of teaching maths offered the most effective approach available.

After extensive consultations with experts in the Singapore method, including Dr. Yeap Ban Har, the first Maths — No Problem! textbooks were introduced in the UK in 2014.

Maths — No Problem! is now an award-winning primary mathematics education programme that combines proven learning theories with advanced mastery teaching techniques.

Maths — No Problem! is the Department for Education’s recommended resource for schools on the government’s Mastery Programme, with textbooks that meet the NCETM’s stringent quality guidelines.

Mark Cotton, principal at Our Lady of Pity RC Primary School, said the Maths — No Problem! programme is “so pedagogically sound” and “completely compelling.”

“I’ve not seen anything like this in education, ever,” he said.

What happens when children don’t master maths

Outcomes are poor for children who struggle with maths concepts and don’t achieve a good grounding in numeracy, according to extensive research.

The Cost of Poor Numeracy

The cost of poor numeracy is well documented, both at the individual and societal level.

Evidence suggests pupils who do poorly in mathematics in primary school are unlikely to do well in secondary school or beyond.

Failing to address numeracy difficulties early leads to greater unemployment, lower income, fewer promotions, along with a host of other more negative outcomes, according to an ECC Trust report.

Although there is a clear correlation between literacy and employment, for numeracy and employment the correlation is even stronger, with nearly four out of ten economically inactive women having very poor numeracy skills and a similar pattern for men, the ECC Trust report said.

A Canadian study found that numeracy is “generally a statistically significant determinant of labour market status, while literacy is most often not statistically significant.”

There’s a strong correlation between numeracy in children and economic performance. Research by Eric Hanushek at Stanford University shows one of the strongest indicators of a country’s GDP growth is the level of cognitive skill in its workforce, as measured by the scores attained by 15-year-olds on international maths tests such as PISA.

What role do teachers play?

Improving mathematics education in all primary schools is therefore an urgent task.

Yet, many teachers:

• Are ill-prepared to teach maths effectively
• Don’t have the necessary skills or resources
• Are generalists
• Lack confidence in their ability to teach maths
• Have a fixed mindset rather than a growth mindset
• Don’t accept that problem solving is at the heart of mathematics.

In addition, teachers who are anxious about or don’t like teaching maths often transfer those feelings to pupils.

What role does the environment play?

On the other hand, teachers may be struggling with the following:

• An ecosystem that doesn’t support them
• An environment that doesn’t encourage them to reflect on and improve their practice
• Being overwhelmed by the weight of expectations placed on them by the system
• Being required to create their own learning materials or to craft their own internal support systems with neither the time nor the expertise to do this properly

Research has repeatedly shown that the order in which pupils are taught various components of a topic will have a massive impact on how deeply they learn.

Yet, cobbling together free lessons from the Internet rarely achieves the correct order. One lesson won’t necessarily lead meaningfully to the next.

This lack of continuity from lesson to lesson, year to year, means mathematics is reduced to a series of unrelated facts.

What tools and resources are available for mastery teaching?

Mastery Tools and Strategies

There are some key strategies, informed by proven theories, that are fundamental to the mastery approach.

CPA Approach

Concrete, Pictorial, Abstract (CPA) is a highly effective approach to teaching that develops a deep and sustainable understanding of maths in pupils. Often referred to as the concrete, representational, abstract framework, CPA was developed by American psychologist Jerome Bruner. It is an essential technique within the Singapore method of teaching maths for mastery.

Concrete is the “doing” stage. During this stage, students use concrete objects to model problems. For example, if a problem involves adding pieces of fruit, children can first handle actual fruit. From there, they can progress to handling abstract counters or cubes which represent the fruit.

Pictorial is the “seeing” stage. Here, visual representations of concrete objects are used to model problems. This stage encourages children to make a mental connection between the physical object they just handled and the abstract pictures, diagrams or models that represent the objects from the problem.

Abstract is the “symbolic” stage, where children use abstract symbols to model problems. Students will not progress to this stage until they have demonstrated that they have a solid understanding of the concrete and pictorial stages of the problem. The abstract stage involves the teacher introducing abstract concepts. Children are introduced to the concept at a symbolic level, using only numbers, notation, and mathematical symbols (for example, +, −, ×, ÷) to indicate addition, subtraction, multiplication, or division.

How to put Bruner’s key theories into teaching practice

The Concrete, Pictorial, Abstract approach lies at the heart of the Maths — No Problem! approach. It enables a natural and supportive progression for learners as they develop their understanding and skills in maths.

For example, to explore equivalent fractions with pupils, the teacher could begin with multi-link cubes, progress to the pictorial problems in the textbook and then on to questions with no visuals except numbers and the necessary mathematical symbols.

This will result in a fully embedded understanding of the concepts throughout the classroom.

Throughout our lives, we all experience this process of learning, revising, and revisiting as we return to old concepts and make sense of new one’s.

Bruner termed this spiralling; the process of coming back to an area of learning to build upon it in light of new discoveries.

Spiralling may also mean we take steps backwards before progressing forward — something to consider when a pupil is not moving forward as we might anticipate.

Bar Modelling

Bar Modelling is an essential maths mastery strategy. A Singapore-style of maths model, bar modelling allows pupils to draw and visualize mathematical concepts to solve problems.

The bar method is primarily pictorial. Pupils will naturally advance from handling concrete objects to drawing pictorial representations to creating abstract rectangles to illustrate a problem.

With time and practice, pupils will no longer need to draw individual boxes or units. Instead, they’ll label one long rectangle or bar with a number.

Bar modelling provides pupils with a powerful tool for solving word problems. However, the lasting power of bar modelling is that once pupils master the approach, they can easily use bar models year after year across many maths topics.

Bar modelling is an excellent technique — though not the only one — for tackling ratio problems, volume problems, fractions, and more.

How to use part–whole bar models in your classroom

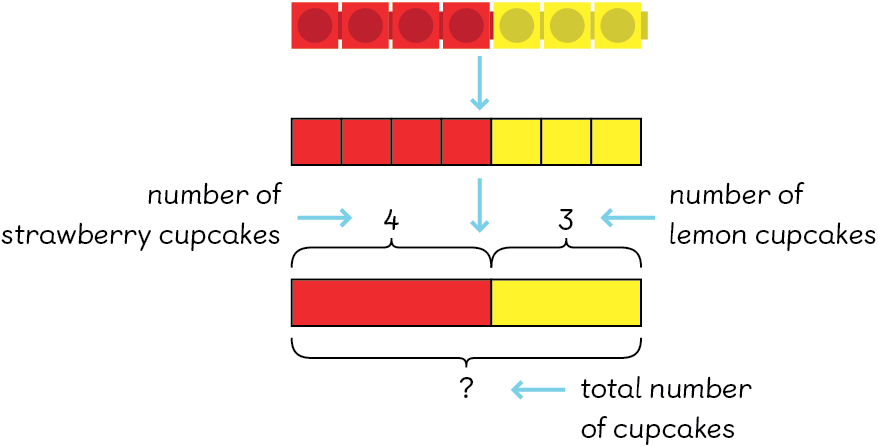
All bar modelling starts with the part–whole model, an essential maths mastery strategy that helps learners visualise the relationships between numbers.

These simple diagrams help learners make the jump from relying on concrete resources to thinking pictorially. Part-whole models are a great way for learners to make sense of a problem and decide which operation they need to use and why.

The part–whole model, sometimes called the part–part–whole model, is a simple pictorial representation of a problem that helps learners see the relationships between numbers. A horizontal bar shows the ‘whole’ amount. Beneath that, an identical bar is divided into pieces to show the ‘parts’ of the whole.

Part–whole bar models illustrate the relationship between what’s known and what still needs to be calculated. The bar can be split into as many parts as necessary. If the total is unknown, you might see the ‘whole’ bar replaced with brackets and a question mark.

Problem solving is always going to be difficult for primary learners. Applying mathematical knowledge can be hard when learners don’t understand which operation they need to use. A part–whole model shows learners the problem in an accessible way.

Part–whole bar models are ideal for:

• Addition
• Subtraction
• Missing numbers
• Division
• Fractions
• Multiplication

They’re particularly useful for time and measurement problems as children often find these problems challenging.

Number Bonds

Number Bonds show how numbers are split or combined. An essential strategy of Singapore maths, number bonds reflect the ‘part-part-whole’ relationship of numbers.

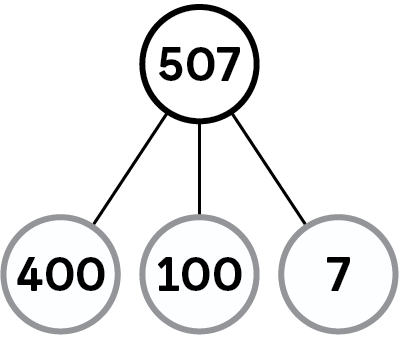
Number bonds let students split numbers in useful ways. They show how numbers join together, and how they break down into component parts.

When used in Year 1, number bonds forge the number sense needed for early primary students to move to addition and subtraction. As students progress, number bonds become an essential mental problem-solving strategy.

Division: Equal Sharing or Equal Grouping?

There are two ways you can approach teaching division: equal sharing and equal grouping.

Children should experience both concepts, but here’s the interesting bit: research suggests that teaching equal grouping before equal sharing will help your pupils develop a deeper understanding of division.

The difference between equal sharing and equal grouping boils down to what the quotient represents. When sharing, the quotient represents the quantity of shared objects in each group. When grouping, the quotient represents the amount of groups within the shared quantity.

At the start of teaching division, teachers often focus on sharing, but not always on grouping. At this stage, it’s important to give equal, or more, emphasis on grouping when pupils are first getting their heads around multiplicative structures.

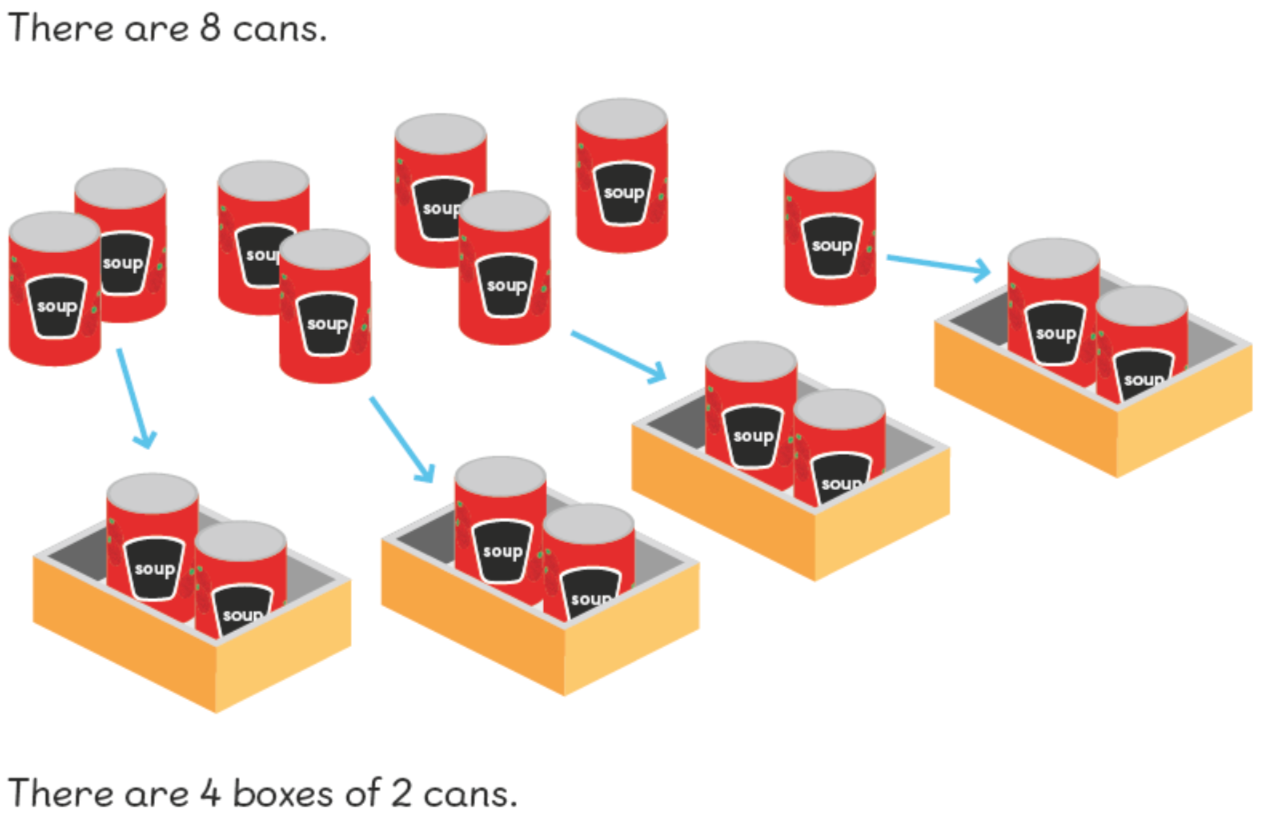
One rationale for this belief is that sharing is more intuitive and it’s likely that pupils already have a notion of sharing — although not necessarily a very deep one.

Grouping is conceptually more difficult and it’s less likely that pupils will have a strong notion of it. Letting them struggle early on with grouping before moving on to the simpler notion of sharing is more likely to create the necessary relational depth.

Number Sense

How important is number sense? Turns out, very.

Number sense is an important construct that separates surface level understanding from subject mastery. So, what is number sense and why is it important for learners to develop this skill?

The construct of number sense refers to fluidity and flexibility with numbers. It helps children understand what numbers mean, improving their performance of mental mathematics and giving them the tools to look at maths in the outside world and make comparisons.

Number sense helps children understand how our number system works, and how numbers relate to each other. Children who develop number sense have a range of mathematical strategies at their disposal. They know when to use them and how to adapt them to meet different situations.

Good number sense helps children manipulate numbers to make calculations easier and gives them the confidence to be flexible in their approach to solving problems.

Children who develop number sense can assess how reasonable an answer is, and routinely estimate answers before calculating. They look for connections and readily spot patterns in numbers, which helps them predict future outcomes. They have several approaches to calculating and problem solving and can use and adapt these for new situations.

Roman Numerals

Children will still see Roman numerals in lots of real-life contexts as they are a rich part of our cultural heritage, they teach basic maths facts, and they can be fun to learn!

Why do children need to learn these cumbersome relics from the past?

Firstly, it’s one of the statutory requirements to ‘read Roman numerals to 100 (I to C)’ in the Year 4 maths programme of study for Number. But, learning Roman numerals is also a great way to help children increase their number sense, better understand how numbers work, and is particularly good for increasing mental maths skills.

Fractions

Understanding fractions is essential to understanding maths generally. But common misconceptions around fractions can leave both teachers and learners feeling more unsure than they should.

Knowing what common misconceptions look like and how to address them can make a significant difference in your learners’ understanding.

For example, why is 1/4 smaller than 1/2? Children learn that 4 is greater than 2. And this is true. So does it also hold true that 1/4 is greater than 1/2?

If you understand the role of the denominator, then this fraction misconception should not exist. However, when you do see this misconception, there are steps you can take:

1. Make the fraction using square or rectangular paper
2. Cut out the pieces
3. Compare the pieces to the written fractions

Can a learner make the connection between the number of pieces it takes to make one whole, and the size of the pieces? Once that connection is made, and the learner has an understanding of what the denominator is telling us, the learner will see that one quarter is smaller than one half.

We could go on to generalise and say the smaller the part is, the more parts will be needed to make one whole.

Conclusion

Well done on making it to the end of our Ultimate Maths Mastery Guide.

We looked at the fundamentals of maths mastery and its relationship to the Singapore method. We discussed the major theorists of the mastery world, and delved into some of the most-effective strategies for mastery teaching.

We also discussed the potential impacts on individuals and society of low maths attainment and poor numeracy.

If you’d like to learn more about maths mastery, we recommend checking out the following links:

• Maths — No Problem! How a growth mindset can transform maths learning
• Maths — No Problem! Senior leadership teams and monitoring mastery
• Elsevier: Changing teacher beliefs around in-class grouping and mindset
• NCETM: Evaluation of the Textbook Project, Year One
• Maths — No Problem! Bar modelling
• Dr. Yeap Ban Har explains bar model basics
• Maths — No Problem! founder Andy Psarianos demonstrates bar models

Also, don’t miss our other Ultimate Guides:

• The Maths — No Problem! Ultimate Guide to Maths Assessment
• The Maths — No Problem! Ultimate Guide to Early Years