How to use journalling to teach multiplication in depth
Editor’s Note:
This is an updated version of a blog post published on November 25, 2019.
Before your learners accelerate to something new, try giving them a journalling activity. Exploring a mathematical topic in depth helps children fully master ideas.
I’m sure you’ve encountered this experience before. A parent informs you that their child is way ahead of their current year group in maths. They’re convinced that, if this child is in Year 4 for example, they need Year 5 or Year 6 work to maintain their level of progress.
The old national curriculum encouraged this idea. Here, learners moved steadily upwards, preferably one level each academic year. Not achieving this in your classroom essentially meant you didn’t maintain their level of progress up to that point.
The new 2014 national curriculum tells a different story; encouraging teaching for depth over acceleration. This framework supports a more forward-thinking approach:
“Pupils who grasp concepts rapidly should be challenged through being offered rich and sophisticated problems before any acceleration through new content.”
Accelerating beyond a child’s age group leads to short-term progress, but it can also mean many basic ideas and procedures aren’t mastered in depth. You’ll see learners’ progress (and presumably confidence) start to tail off.
The path to mathematical fluency isn’t a series of linear levels. Think of it as a web where learners can identify and link together multiple methods and patterns to fully embed understanding.
How do you use journalling to teach multiplication for depth?
When teaching Year 6 multiplication, the 2014 national curriculum expects that:
“Pupils practise and extend their use of the formal written methods of short multiplication… apply all the multiplication tables… and use them confidently to make larger calculations.”
So, how can you encourage depth when looking at multiplication? I have one word for you: journalling.
The five different types of journalling (descriptive, evaluative, creative, investigative, and formative) can be used in different ways. Maths journals do more than just let learners record their answers, they give learners a place to practice communicating their thoughts and ideas. Journals give insight into how children are thinking and provide evidence that learners are developing their understanding.
Journalling lends itself to a wealth of ideas and approaches and can be a powerful tool when teaching for depth. Let’s look at a few practical examples for learners in Year 6. These examples are helpful for teaching Key Stage 2, but can be adapted for learners across the years.
The following lesson comes from Maths — No Problem! Textbook 6A, Chapter 2, Lesson 5 and the list of questions in the Guided Practice. I’ve rounded up a few interesting examples from learners who are competent in the four number operations.

1. Creative journalling: linking a calculation to a real-life problem
The original calculation was: 311 × 32 = ?
In this maths journal example, the learner thought the original calculation should be trickier to find than the modelled examples in the anchor task. They added an extra challenge for themselves by carefully constructing a word problem so you had to do an addition and a subtraction before you tackle the multiplication part.
Using a real-life context for a calculation helps build problem-solving skills. Asking children to create a scenario that fits with a calculation takes the level of challenge even further.

Bumbles is a caretaker at a school, on the schools open morning, he prepares from the clean up job. He knows that 6,941 people are coming. Each person receives one pencil, two rulers, ten letters from staff and 19 pieces of a puzzle. 6,630 people take their gifts home, but the remainder don’t, and leave them on the playground. How many pieces of gifts will Bumbles have to clear up?
Their answer
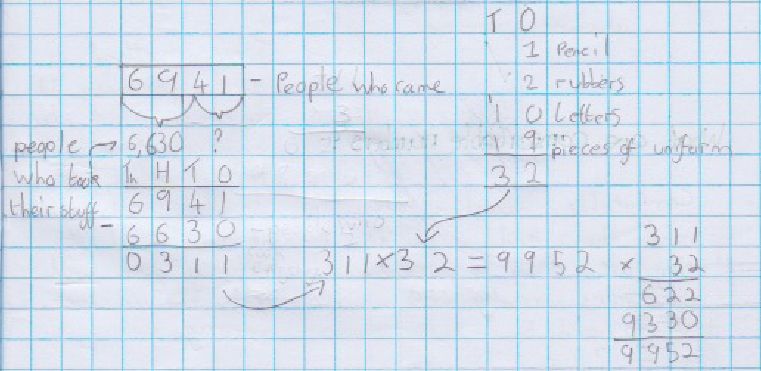
Boost Your Practice with FREE CPD
Receive a CPD boost every time you refer a school! Both you and the referred school will earn a full day of CPD and 2 free places on our 3-day Essentials of Teaching Maths Mastery course (valued at £1700).
Get started on helping struggling schools reach maths success now!

2. Creative journalling: add something new to a modelled example
The original calculation was: 420 × 20 = ?

Here the child used the standard written method to show the answer to 420 × 20. However, they broadened the scope of the question really well by making it a two-step word problem.
When teaching a problem like this, you can encourage variations that involve larger calculations by choosing different months or even an entire year. After extending the original question, this learner chose to make the maths bilingual and wrote the problem in his native language — Arabic!

By skipping ahead to Year 7 topics, learners would miss out on chances to build connections between the maths they are learning and the real-world. The more time learners spend exploring a topic in depth and applying it to different contexts, the more secure their learning becomes.
3. Descriptive journalling: organise information to support understanding
The original calculation was: 432 × 22 = ?
In this example, the child showed that alongside the standard written method of multiplication, you could split the 22 or the 432 if you wanted a harder challenge. One method was his preferred choice, and he used the second to check. His third choice was just to show it could be done!

Learners with less maths confidence made a straightforward word problem or took one of the simpler examples like multiplying by 20. Maybe they couldn’t reach the same heights as their more advanced peers, but their journalling showed that they still understood the non-negotiable learning objective: one method of multiplying two-digit numbers.
Giving learners the chance to develop their understanding of the four operations helps to build their fluency. Once they can use a method efficiently, move flexibly between methods, and use different methods to double check their answer, you’ll know they’ve achieved fluency.
4. Evaluative journalling: make a choice between competing methods and offer reasons for choices
The original calculation was: 210 × 42 = ?
In this example, I asked learners who had operated both methods to consider the positives and negatives for long multiplication and splitting numbers.
The learners appreciated that formal written methods give them a way that works every time — if you lay out the calculation properly and carry the digits correctly.
The learners split the calculation in different ways — one splitting 210 into 200 and 10, and the other splitting 20 in 10 and 10. They both pointed out that the individual calculations are easier because you are multiplying ‘comfortable’ numbers like 2, 5, and 10.
One of the learners pointed out that you run the risk of splitting the number incorrectly while another thought that the method wouldn’t be helpful for numbers that are harder to split.


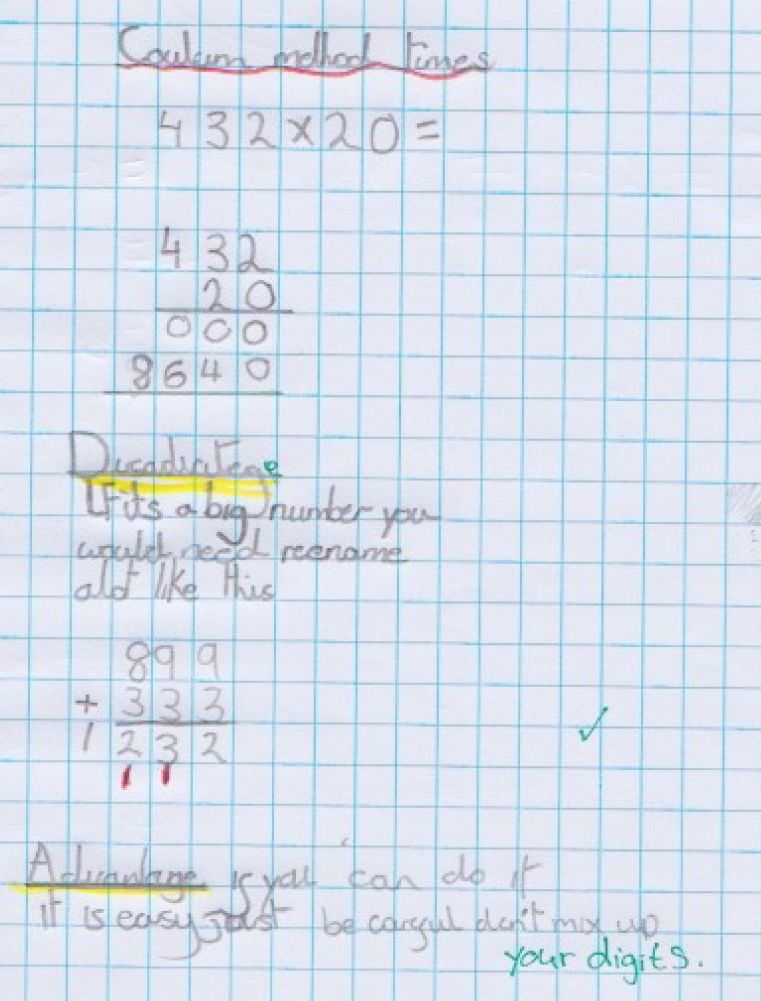
It’s one thing to be fluent in different calculation methods, but the skill of weighing up the method’s pros and cons needs a much deeper level of understanding. It also helps learners to choose more efficient strategies when solving problems in the future.
Depth through journalling vs. acceleration
Journalling encourages depth, helps learners gain fluency in multiplication, and tackles a mathematical topic in a way that allows later progression. It’s also a great way to stretch learners by showing maths in a variety of contexts with realistic problems.
Using journalling as an alternative to acceleration helps learners develop flexible-thinking skills and the confidence to tackle new concepts in the years ahead.
